Как рассчитать процент в калькуляторе с помощью процентного ключа
Процентная клавиша на калькуляторах не является новой функцией. Это очень помогает нам, когда мы хотим быстро рассчитать процент, чтобы узнать, сколько мы получаем, теряем или сколько процентов мы должны кому-то платить. Не слишком углубляясь в математику, здесь мы узнаем простой метод вычисления процента некоторых данных с использованием простой опции, т. Е. Ключа процента в калькуляторах.
Действительно, когда мы думаем или слышим слово калькулятор, первое, что приходит в голову, это карманный калькулятор с жесткими клавишами. Тем не менее, настоящие аппаратные калькуляторы в настоящее время используются меньше из-за распространенности smartphones и компьютерные программные калькуляторы.
Таким образом, если вы ищете калькулятор, чтобы узнать процентный расчет сегодня, вы редко думаете о реальном калькуляторе, который вы кладете в карман. Вместо этого большинство из них используют программы с богатым интерфейсом, с помощью которых мы можем не только рассчитать процент, но и научный расчет.
Процент расчета шагов с использованием ключа
Здесь мы используем Windows 10 программный калькулятор, который работает именно на реальном оборудовании карманный калькулятор и даже шаги, приведенные ниже, чтобы узнать процент будет одинаковым на обоих даже на научный один.
открыто Windows 10 или 7 калькулятор
Первый шаг к определению процента – это доступ к калькулятору. Если у вас есть Windows 10/8/7 тогда вам не нужно никуда идти, у вас уже есть очень хороший калькулятор с функцией процентного ключа. Не только % функция, но она может быть использована в качестве Данные а также научный калькулятор плюс конвертер (Валюта, объем, длина, вес, масса, температура и многое другое …).
Чтобы получить доступ к нему на Windows 10 или 7, нажмите кнопку «Пуск» и введите калькулятор.
Запустите стандартную программу калькулятора
На приведенном выше шаге, когда мы ввели «калькулятор», Появится несколько вариантов, нажмите стандарт вариант.
Введите начальное значение, чей процент вы хотите узнать?
Введите значение или число, процент, который вы хотите рассчитать. Например, я хочу найти 25 процент от числа 1200, Таким образом, первое число, которое я наберу на калькуляторе, будет 1200,
Умножьте сумму процентов на начальное значение
Теперь нажмите или нажмите Умножить ключ функцию и введите количество процентов, которые вы хотите рассчитать. Например, я хочу узнать 25% из 1200, Итак, у меня уже есть тип 1200 в вышеприведенном шаге сейчас я нажму ключ умножения а потом наберете 25 (процентное значение или значение).Короче: 1200 х 25
Нажмите или нажмите на кнопку процента, чтобы рассчитать его
Итак, мы уже умножили наши два значения, начальное значение на сумму процент мы хотим выяснить. Уравнение было похоже1200 х 25, теперь нажмите процентный ключ показ % знак. Расположение ключа может отличаться на вашем устройстве, но знак будет таким же.
Таким образом, шаги, которые мы проделали до сих пор в одном уравнении: 1200 × 25%
Нажав на знак равенства, вы получите результат
В тот момент, когда мы нажимаем на Процентный ключ калькулятор автоматически рассчитает процент нашего желаемого числа. Теперь просто нажмите на знак равенства, вы получите результат.
Наш результат: 1200 × 25% = 300
Например, вы можете определить процент от вашей цифры, просто замените приведенные здесь значения на те, которые вы хотите вычислить.
Другой пример– Мы хотим узнать 0.2% от 50.Введите 50 умножьте на 0,2 и нажмите кнопку =.50 х 0,2% = 0,1
Таким образом, мы можем вычислить процент числа, используя клавишу%. Кроме того, вы можете переключаться между научным режимом, вариантом для программистов, вычислением даты и различными функциями преобразования, используя значок с тремя строками или бургер, указанный в верхней левой части окна. Windows Программа 10 калькуляторов.
Как посчитать проценты на калькуляторе?
Посчитать проценты на калькуляторе очень просто. Например, вам нужно посчитать сколько будет 30% от числа 60. Наберем вначале число 60 цифрами. Вначале нажимаем цифру шесть (6), а потом уже ноль (0). Дальше нужно нажать знак умножить. Обычно он выглядит как буква Х (ха или икс). Не путайте, пожалуйста, с плюсом, который рисуется как небольшой крестик! Иначе не получится ничего у нас не получится. Следующим действием набираем 30 — вначале 3, а потом 0. И наконец, нажимаем на знак % (процента). Все, не нужно нажимать равно! У вас уже получился готовый результат. Перепроверьте должно получиться число 18.
Как посчитать проценты: от числа, от суммы чисел и др. [в уме, на калькуляторе и с помощью Excel]
Проценты, скажу я вам, это не только что-то «скучное» на уроках математики в школе, но еще и архи-нужная и прикладная вещь в жизни 👌 (встречаемая повсюду: когда берете кредит, оцениваете скидку, считаете прибыль и т.д.).
И на мой взгляд, при изучении темы «процентов» в той же школе — этому уделяется чрезвычайно мало времени. Возможно, из-за этого, некоторые люди попадают в не очень приятные ситуации (многие из которых можно было бы избежать, если бы вовремя прикинуть что там и как. ).
Собственно, в этой статье хочу разобрать наиболее популярные задачи с процентами, которые как раз встречаются в жизни (разумеется, рассмотрю это как можно на более простом языке с примерами). Ну а предупрежден — значит вооружен 😉 (думаю, что знание этой темы позволит многим сэкономить и время, и деньги).
И так, ближе к теме.
Как посчитать проценты: примеры
Вариант 1: расчет простых чисел в уме за 2-3 сек.
В подавляющем большинстве случаев в жизни требуется быстро прикинуть в уме, сколько там это будет скидка в 10% от какого-то числа (например). Согласитесь, чтобы принять решение о покупке, вам ненужно высчитывать все вплоть до копейки (важно прикинуть порядок).
Наиболее распространенные варианты чисел с процентами привел в списке ниже, а также, на что нужно разделить число, чтобы узнать искомую величину.
- 1% от числа = разделить число на 100 (1% от 200 = 200/100 = 2);
- 10% от числа = разделить число на 10 (10% от 200 = 200/10 = 20);
- 25% от числа = разделить число на 4 или два раза на 2 (25% от 200 = 200/4 = 50);
- 33% от числа ≈ разделить число на 3;
- 50% от числа = разделить число на 2.
Задачка! Например, вы хотите купить технику за 197 тыс. руб. Магазин делает скидку в 10,99%, если вы выполняете какие-нибудь условия. Как это быстро прикинуть, стоит ли оно того?
Пример решения. Да просто округлить эти пару чисел: вместо 197 взять сумму в 200, вместо 10,99% взять 10% (условно). Итого, нужно-то 200 разделить на 10 — т.е. мы оценили размер скидки, примерно в 20 тыс. руб. (при определенном опыте расчет делается практически на автомате за 2-3 сек.).
Точный расчет : 197*10,99/100 = 21,65 тыс. руб.
Диаграмма с процентами / в качестве примера
Вариант 2: используем калькулятор телефона на Андроид
Когда результат нужен более точный, можно воспользоваться калькулятором на телефоне (в статье ниже приведу скрины с Андроида). Пользоваться им достаточно просто.
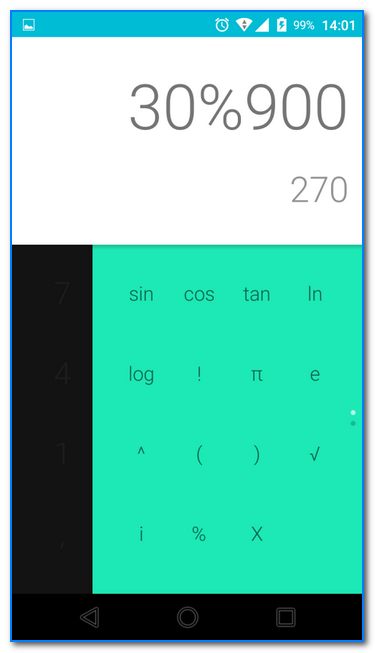
Например, вам нужно найти 30% от числа 900. Как это сделать?
Да достаточно легко:
- открыть калькулятор;
- написать 30%900 (естественно, процент и число может быть отличными);
- обратите внимание, что внизу под вашим написанным «уравнением» вы увидите число 270 — это и есть 30% от 900.
30% от числа 900 (калькулятор Андроид)
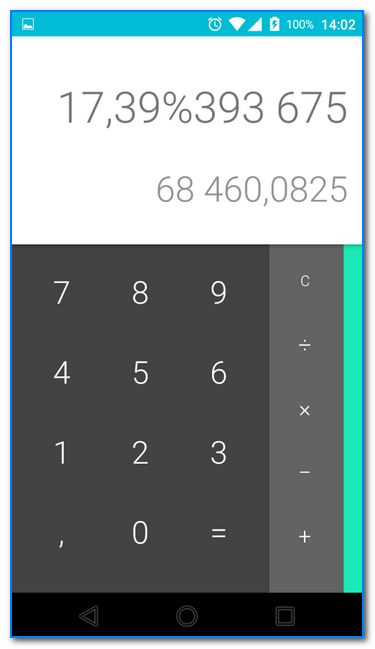
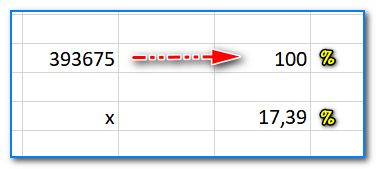
Ниже представлен более сложный пример. Нашли 17,39% от числа 393 675 (результат 68460,08).
еще один пример
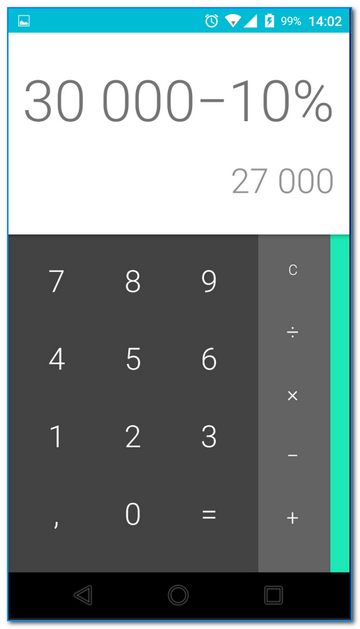
Если вам нужно, например, от 30 000 отнять 10% и узнать сколько это будет, то вы можете так это и написать (кстати, 10% от 30 000 — это 3000).
Таким образом, если от 30 000 отнять 3000 — будет 27000 (что и показал калькулятор). 👇
От числа отнимаем 10% (еще один пример)
В общем-то, весьма удобный инструмент, когда нужно просчитать 2-3 числа и получить точные результаты, вплоть до десятых/сотых.
Вариант 3: считаем процент от числа (суть расчета + золотое правило)
Не всегда и не везде можно округлять числа и высчитывать проценты в уме. Причем, иногда требуется не только получить какой-то точный результат, но и понять саму «суть расчета» (например, чтобы просчитать сотню/тысячу различных задачек в Excel).
В этих случаях рекомендую запомнить одно «золотое» правило столбика. Если вы поймете его — то без проблем сможете всегда решать задачки с процентами.
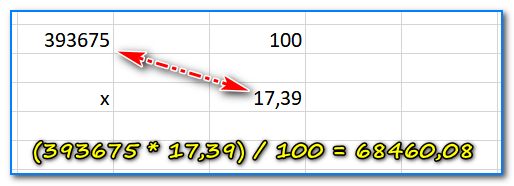
Допустим нам необходимо найти 17,39% от числа 393 675. Решим эту простую задачку.
- сначала запишите на листочке число 393675 и напротив него напишите 100% (т.е. число, от которого мы пытаемся найти какой-то процент — считаем за 100%) ;
- далее под 100% напишите, тот процент, который хотите найти (т.е. 17,39 в нашем примере); под самим числом — поставьте «X» (т.е. то число, что нужно найти, см. скрин ниже). Здесь главное число писать под числом, проценты под процентами (и не путать между собой их)!
Записываем числа для расчета процентов
Крест на крест (считаем проценты)
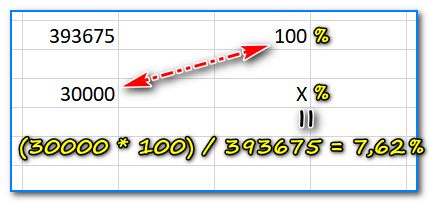
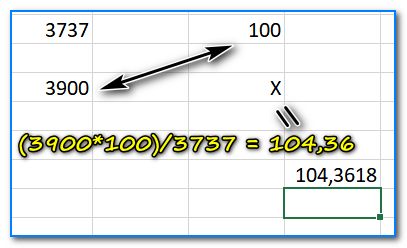
Чтобы снять все точки на «Й», рассмотрю обратную задачу. Например, сколько процентов составляет число 30 000 от числа 393 675.
- сначала записываем столбиком также 393 675 и напротив него ставим 100%;
- далее под самим числом 393 675 пишем 30 000, а напротив него ставим X (т.е. то, что нам нужно найти);
- далее (30 000 * 100)/393675 и получаем 7,62 % (можете проверить 👌). Т.е. работает тоже правило: перемножаем крест на крест (т.е. там, где в диагонали известны два числа) и делим на оставшееся. Таким образом легко найти неизвестное.
Обратная задачка с процентами
Вариант 4: считаем проценты в Excel
Excel хорош тем, что позволяет производить достаточно объемные расчеты: можно одновременно просчитывать десятки самых различных таблиц, связав их между собой. Да и вообще, разве вручную просчитаешь проценты для десятков наименований товаров, например.
Ниже покажу парочку примеров, с которыми наиболее часто приходится сталкиваться.
Задачка первая. Есть два числа, например, цена покупки и продажи. Надо узнать разницу между этими двумя числами в процентах (насколько одно больше/меньше другого).
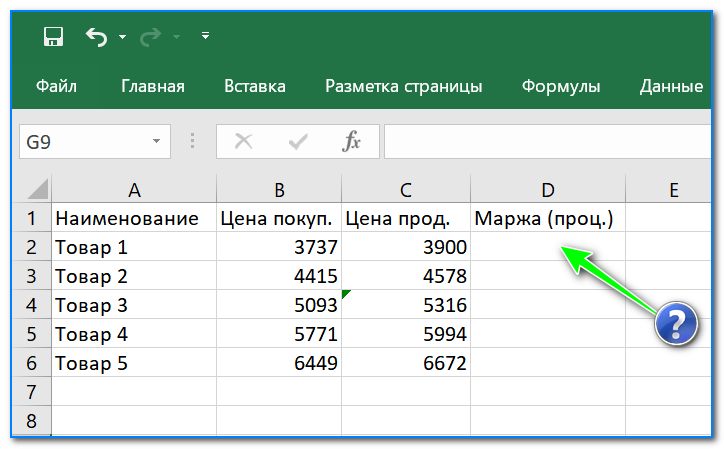
- Сначала оформляем все это в Excel в форме таблички (пример см. ниже: в моем случае будем считать проценты для столбика «Маржа» по цене покупки и цене продажи товара) ;
Как определить, насколько одно число больше другого в процентах
Второе число составляет 104% от первого
Формулу растянули — проценты посчитаны для всего столбца
Для более точного понимания, приведу еще один пример. Другая задачка: есть цена покупки и желаемый процент прибыли (допустим 10%). Как узнать цену продажи. Вроде бы все просто, но многие «спотыкаются».
Инструкция по расчету процентов от числа на калькуляторе
Термин «процент» происходит от латинского словосочетания «pro centum» — «на сто, сотая», и означает «сотую часть». Сравните английское «per cent». Для обозначения процента используется символ «%», который показывает долю чего-либо по отношению к целому. Например, 32% пройденного пути от расстояния в 67 км будут означать 32 отрезка по 0,67 км, т. е. 32×0,67=21,44 км. Знак «%» произошёл от итальянского сокращения pc — per cento.
Три типа задач на проценты
Для всех видов практических задач на проценты используется универсальная формула:
где р — процент, который число А составляет от числа В. (1).
Величину р следует трактовать здесь как количество сотых долей, которые число, А составляет от числа В. Пользуясь этой формулой, можно решать три типа задач, по числу неизвестных в ней.
Задачи первого типа
Здесь необходимо найти неизвестное число процентов. Для этого используется формула (1). Вот простейший пример: сколько % от 25 составляет число 12,5?
Задачи второго типа
Нужно найти, сколько будет р % от числа В. Из (1) можно легко получить следующую формулу:
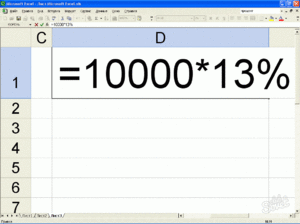
Задача. Сколько будет 13% от 6700 рублей?
Решение: А=(13/100)x6700=871 рубль.
Задачи третьего типа
Если известно, что р % от числа В равно А. Чему равно В? Из (1) следует, что
Задача. 7% от некоторого числа равно 777. Чему равно само число?
Решение: В=(100×777)/7=11100.
Инструкция по расчету процентов на калькуляторе
Чтобы решать подобные задачи, вовсе не нужно помнить наизусть весь школьный курс арифметики. Конечно, если вам до сих пор знакомы «любимые» вами пропорции, вы можете воспользоваться ими. Но если у вас есть калькулятор (бухгалтерский, или в операционной системе вашего компьютера), на котором есть клавиша «%», то все указанные действия вы легко сможете проделать с его помощью. Советы, как посчитать проценты от суммы на калькуляторе, непременно помогут вам в каждой конкретной ситуации. Вот вам простая инструкция, как это сделать.
- Чтобы узнать, сколько процентов р величина А составляет от величины В, введите А, нажмите «÷», затем введите В и нажмите «%» и «=». Пример: «2÷5%=». Результат на дисплее: 40.
- Чтобы узнать, чему равны р процентов от величины В, введите число р, нажмите «%», затем введите число В и нажмите «=». Пример: «13%91=». Итог на дисплее: 11,83.
- Чтобы узнать, чему равно число В, если р процентов от него составляют величину А, то введите А, нажмите «÷», введите р и нажмите «%». Пример: «12÷12%». Итог на дисплее: 100.
Простые и сложные %
Рассмотрим ещё тип задач, относящихся к финансовым и связанных с процентами. Это такие задачи, в которых нужно вычислять доход от вклада или инвестиций. Вот такой пример. Вы вложили деньги в банк под р % годовых некую сумму S0. Чему будет равен ваш капитал через n лет? И ответ на этот вопрос зависит от того, какой у вас вклад: с простым начислением процентов или с их капитализацией.
Простое начисление процентов — это ежегодное (ежеквартальное, ежемесячное) получение р % от суммы вашего вклада, когда начальная сумма вклада S0 фиксирована, а вы регулярно с этой суммы получаете фиксированный доход, то есть каждый год (квартал, месяц) вы получаете прибыль 0,01p•S0. Через n лет ваша прибыль станет равна 0,01nр•S0. Полученная прибыль суммируется с вашим начальным вкладом S0, в результате чего вся сумма прибыли вместе с процентами составит:
Задача. Вы положили 100000 рублей в банк под 10% годовых на 5 лет. Чему станет равен ваш вклад?
Решение: S=100000•(1+0,01•5•10)=100000•1,5=150000 рублей.
Допустим теперь, что ваш вклад с капитализацией процентов. Это означает, что после каждого начисления проценты прибавляются к уже имеющейся сумме на вашем счету. Таким образом, после следующего начисления сумма процентов становится больше. Например, в первый год проценты по вкладу с капитализацией составят 0,01р•S0, а за второй год эта сумма будет уже больше и составит 0,01p•(S0+0,01p•S0)=0,01p•S0•(1+0,01р), а за третий год — 0,01p•(S0+0,01p•S0•(1+0,01р))=0,01р•S0•(1+0,01p+(0,01p)²).
Выражение в скобках представляет собой сумму геометрической прогрессии, которая равна (0,01р)². Поэтому за третий год сумма на вашем счету станет равной S0+S0•(0,01р)³. Продолжая так дальше, через n лет или периодов начисления, сумма на счету вместе с начисленными процентами составит:
S=S0•(1+0,01р)ⁿ. (5).
Мы получили так называемую формулу сложных процентов, которая позволяет высчитывать сумму на вашем счету по вкладу с капитализацией процентов.
Задача. Вы положили всё те же 100 000 рублей на 5 лет под 10 % годовых, но открыли вклад с капитализацией. Сколько к концу указанного срока будет на вашем счету?
Решение. Пользуясь формулой сложных процентов, получим: S=100000•(1+0,01•10)^5=100000•1,1^5=100000•1,61051=161051 рубль.
Сравнивая результаты, полученные по формулам (4) и (5), видим, что по вкладу с капитализацией сумма на счету стала больше на 11051 рубль по сравнению с обычным вкладом, где происходит простое начисление процентов. Таким образом, второй способ вложения денег выгоднее.
Примеры задач
Как рассчитать стоимость кредита
Если вы хотите приблизительно знать, во сколько вам обойдётся банковский кредит, который вы берёте, вот вам простая формула:
- полная стоимость кредита=сумма кредита×[1+0,01×ставка по кредиту×срок кредитования]
Эта формула, как вы понимаете, не учитывает комиссий, платы за обслуживание кредита, страховых взносов, штрафов за просрочку, пени и прочих расходов. Но вы всё равно можете ею пользоваться, чтобы грубо оценить полную стоимость вашего кредита.
Задача. Вы хотите взять 10 млн рублей в ипотеку под 10 % годовых на срок 15 лет (допустим, первый взнос вы уже внесли). Во сколько вам обойдётся данный кредит?
Решение. Полная стоимость кредита составит 10 млн × (1+0,01×10×15)=10 млн × 2,5=25 млн рублей, то есть вам придётся заплатить общую сумму в 25 млн рублей, в которую, помимо суммы долга в 10 млн рублей, входит сумма процентов за пользование кредитом, равная 25–10=15 млн рублей, или 1 млн рублей в год.
Как рассчитать сумму комиссии
Часто нам приходится оплачивать мобильную связь, пополнять электронные кошельки, совершать те или иные платежи. Во всех случаях присутствует тот или иной процент комиссий за пользование сервисом. Как быть, если вы хотите точно знать, какая сумма ляжет вам на счёт или на баланс, или же спишется с вашего электронного кошелька в результате комиссий? Ответ прост. Используйте калькулятор или ваш ум, а также приведённую выше инструкцию вместе со следующей формулой:
- сумма с учётом комиссии=требуемая сумма×[1+0,01×процент комиссии] + фиксированная комиссия
Задача. Какая сумма спишется с баланса мобильного при пополнении с него электронного кошелька, если вы хотите положить на кошелёк 100 рублей, причём комиссионный процент равен 8 %, а фиксированная комиссия составляет 10 рублей?
Решение. Сумма с учётом комиссии будет равна 100×(1+0,01×8)+10=100×1,08+10=118 рублей. Именно такую сумму нужно указать в платежной форме, чтобы у вас на кошельке появились 100 рублей.
Рентабельность вашего бизнеса
Как рассчитать эффективность вашего бизнеса? Для этого нужно знать обобщённые показатели деятельности фирмы, которой вы руководите, такие, как валовая прибыль за прошедший период (который может составлять месяц, квартал, полугодие, год) и общие затраты за тот же период. Тогда вы сможете найти рентабельность вашей деятельности, которая показывает чистую прибыль на 1 рубль затрат:
- рентабельность=[(валовая прибыль – общие затраты)/общие затраты]×100 %
Задача. Валовая прибыль вашего бизнеса за прошедший год составила 10 млн рублей при общих затратах в 8 млн рублей. Чему равна рентабельность бизнеса за прошедший год?
Решение. Рентабельность бизнеса равна [(10 млн – 8 млн)/8 млн]×100 %=0,25×100 %=25 %, т. е. на каждый вложенный рубль вы получили доход в 25 копеек.
На сколько % перевыполнен план
Если нужно узнать, насколько величина А больше величины В в процентном отношении, то пригодится следующая формула:
- увеличение (прирост) А по сравнению с В=[(А – В)/В]×100 %
Задача. Завод запланировал в текущем квартале выпуск 300 тыс. подшипников, но фактически было произведено 420 тыс. подшипников. На сколько процентов был перевыполнен план по выпуску изделий?
Решение. План за квартал был перевыполнен на [(420 тыс. – 300 тыс.)/300 тыс.]×100 %=
На сколько % упала прибыль
Когда вы хотите знать, на сколько величина А меньше величины В в процентном отношении, воспользуйтесь следующей формулой:
- уменьшение А по сравнению с В=[(В – А)/В]×100 %
Задача. Прибыль вашего предприятия за последний месяц снизилась со 100 тыс. рублей до 90 тыс. рублей. На сколько процентов упала прибыль за прошедший месяц?
Решение. Снижение прибыли составило [(100 тыс. – 90 тыс.)/100 тыс.]×100 %=10 %.
Download Article
Download Article
A percentage is a special way of representing a portion of something. A percentage is a number that indicates a fraction made up of 100 parts. Thus, 100% means the whole thing (whatever is being measured), while 50% means one half. If you learn how to write numbers as percentages, it then becomes easy to perform multiplication and other calculations with percentages on a calculator. Some calculators even have a % button that makes the calculation even easier.[1]
-
1
Review the general meaning of fractions. A fraction is a comparison between two numbers, usually representing the size of a part of something to the size of the whole thing. The classic example is a pie that is cut into eight, for example, equal portions. The top of the fraction, called the
numerator, represents the number of pieces you select.
The bottom of the fraction, called the
denominator, represents the total number of pieces in the pie
— in this case, 8.[2]
- For example, the fraction 1/8 represents one piece of the pie that has been cut in eight pieces.
- The fraction 7/8 represents 7 pieces, almost the full pie.
-
2
Recognize the special relationship of percentages. A percentage is a special kind of fraction in which the
denominator is always set at 100.
[3]
While this is not practical when cutting slices of an actual pie, the concept of percentages is much more useful because it is standard.- With fractions, the size of “half” of something will depend on the number of pieces. If your “pie” is cut into 8 pieces, then half would be 4. But if your “pie” is in 22 pieces, then half would be 11. The target always changes. But with percentages, one-half is always the same — 50%.
- It’s helpful to remember that the word «percent» actually means «of 100″—»per» means «of,» and «cent» means «100.»[4]
Advertisement
-
3
Use a calculator to convert any fraction to a decimal or percentage. If you are presented with any fraction, you can very easily convert it to a decimal number using any calculator. Just recognize that a fraction represents a division problem, and
use your calculator to divide the numerator by the denominator.
Your calculator will give you the decimal equivalent of the fraction.[5]
- Suppose you have the fraction 1/2. On your calculator, perform the operation 1 ÷ 2, and the calculator will show the result 0.5.
- Convert the fraction 1/4 into a decimal by performing the operation 1 ÷ 4. The result is 0.25.
- For a more complicated example, you can convert the fraction 274/312 into a decimal with the operation 274 ÷ 312. The result will be 0.878. (There are more digits, but for our purposes we can stop at three.)
-
4
Convert decimals to percentages by shifting the decimal point. If you have a number that is already represented by a decimal, converting that to a percentage is easy. Because the decimal numbering system is based on factors of 10, you can transform a decimal number into a percentage by simply
shifting the decimal point by two spaces to the right and then adding a % sign.
If your decimal number consists of only one digit, you can add 0’s on the right of the number, such as turning 0.5 into 0.50 or even 0.500. These all have the same numerical value.[6]
- Consider the example above of 1/2, which we converted to the decimal of 0.5. To change this decimal to a percentage, shift the decimal point two spaces to the right. First rewrite 0.5 as 0.50. Then when you shift the decimal point two spaces, you turn 0.50 into the number 50%.
- The example of 1/4, which has a decimal equivalent of 0.25, can be turned into the percentage 25%.
-
5
Memorize basic fraction conversions. It is useful if you can memorize the percentage representations of certain basic fractions. Because the denominator for a percentage is always 100, certain values are constant. Some basic conversions you should know include:[7]
- 3/4 = 75%
- 1/2 = 50%
- 1/3 = 33 1/3%
- 1/4 = 25%
- 1/5 = 20%
- 1/8 = 12.5% (this is often used in banking)
Advertisement
-
1
Add percentages very directly. Because percentages all represent fractions with the common denominator of 100, you can add a list of percentages without any additional work. By contrast, remember that to add fractions, you must work through the steps of finding common denominators and converting your fractions to those common denominators. With percentages, however, no additional work is necessary.[8]
Just add the numbers together.
- If each of six people draws a portion of the company’s payroll, you can find out how much they represent together by just adding the relative percentages. If their respective shares are 10%, 5%, 8%, 22%, 10% and 8%, you can just add 10+5+8+22+10+8 = 63. Those six people make up 63% of the company’s payroll.
- When you are adding, ignore the percent symbol, and just add the numbers. Put the symbol back in your final answer.
-
2
Subtract percentages in the same manner. Again, because percentages represent fractions with the common denominator of 100, you do not need to do any additional work to subtract percentages. If you are working the the concept of removing some percentage from an original whole item, you should represent the whole item with the number 100 (because the whole means 100%).[9]
- Suppose you want to calculate an income percentage. 100% represents the entire income from some project, but then you must subtract, for example, 10% for expenses, 12% for salaries, and 25% for taxes. How much is left? Simply use your calculator to perform the subtraction of 100-10-12-25. The result is 53%.
-
3
Multiply or divide using decimal equivalents. If you have a problem that is initially written as 25% x 30, just
write the 25% as its decimal equivalent 0.25 and conduct the operation.
This would be 0.25 x 30 which gives the result of 7.5.[10]
Similarly, if you have a division problem of 200 ÷ 10%, rewrite this as 200 ÷ 0.10 and enter this into your calculator. You will get the result of 2000.[11]
- The last result may appear surprising, if you expect division to produce a smaller result than the starting number. However, you should understand that division by a number less than one will always lead to an increase by the reciprocal of that number. For example,
dividing by 1/10 is the same as multiplying by 10.
Dividing by 1/2 is the same as multiplying by 2.
- The last result may appear surprising, if you expect division to produce a smaller result than the starting number. However, you should understand that division by a number less than one will always lead to an increase by the reciprocal of that number. For example,
Advertisement
-
1
Perform multiplication to find the percent “of” a number. A common calculation involving percentages is to find some percent “of” another number. For example, if you are in a restaurant you may want to tip 15% “of” your total bill. When working with percentages,
the word “of” carries the same meaning as “times” or “multiply.”
Therefore, 15% “of” 100, for example, means the same as 15% x 100.[12]
-
2
Convert the percentage to a decimal and multiply. To calculate the percentage of the whole number, you need to first turn the percentage into a decimal as already described. Then simply multiply.[13]
- To find 15% of 100, rewrite the 15% as 0.15. Then just multiply 0.15 x 100, to get the solution of 15.
-
3
Write your result without a percentage symbol. When you set out to find a percentage of a whole number,
your result will be a number and not a percentage.
You may begin with a percentage symbol, but when you convert that percentage to a decimal to conduct the multiplication, your answer will no longer have a percentage symbol.[14]
- In the example of 15% of 100, the result is the whole number 15.
Advertisement
-
1
Find the % key on your calculator. Most simple calculators will contain a key with the % symbol. More advanced, graphing calculators may not have this key because the makers expect that you can operate without it. But many more basic calculators will have it.[15]
-
2
Experiment with the % key for decimal conversions. The simplest use of the % key is to
convert any number from its percentage form to its decimal form.
Just enter the number and press the % button, and the calculator will show the decimal equivalent.
- To represent the number 4% on your calculator, just press the button 4 and then %. Your calculator will turn the number 4 into 0.04, which is the decimal equivalent.
- To change the number 82.5% into a decimal, just type the buttons 8, 2, . , 5, %. The calculator will now show the value of 0.825.
-
3
Use the % key for calculations. The % key on your calculator makes certain calculations very simple. Suppose you want to calculate a tip amount, and you want to find 15% of the total bill of $75.32. If you have your calculator available, you will enter the buttons 15% x 75.32. You should get the result of 11.298, which represents a tip of $11.30.[16]
- Whenever you are using a calculator for percentage calculations, you should make sure to press the Clear (C) or All Clear (AC) button before starting.
- As you enter the numbers for this calculation, you should notice that as soon as your hit the % button, your number of 15 converts to .15. The calculator will the proceed to calculate .15 x 75.32.
Advertisement
Add New Question
-
Question
How do you easily add the tip to a bill at a restaurant?
David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Academic Tutor
Expert Answer
Support wikiHow by
unlocking this expert answer.You can easily calculate your total bill including a tip or a tax by adding 1 to the percentage. For example, if you have a $20 meal and you want to add 15% to the bill, multiply $20 by 1.15 to get $23. That’s faster than figuring out 15% of $20, which is $3, then adding it back to $20.
-
Question
How do you take a percent of a number that isn’t 100?
David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Academic Tutor
Expert Answer
Support wikiHow by
unlocking this expert answer.If you have a problem like «What’s 25% of 50?» turn the percent into a decimal. In this case, 25% is the same as 0.25. Then, you’d multiply that by the second number—0.25 times 50, which is 12.5.
-
Question
What is 6% off 299.00?
Multiply 299.00 by 0.06 to get the amount of the discount. Subtract that amount from 299.00 to find the number that replaces 299.00.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Things You’ll Need
- Calculator
- Pencil
- Paper
References
About This Article
Article SummaryX
To do percentages on a calculator using the percentage button, enter the percentage times the original number. For example, if you wanted to give a waiter a 20% tip on your $50 order, you would enter 20 and hit the percentage button to get 20%. Then you would hit the multiplication button, enter 50, and hit the equals button to find that 20% of $50 is $10. Read more to learn how to find percentages without using the percentage button!
Did this summary help you?
Thanks to all authors for creating a page that has been read 452,740 times.
Reader Success Stories
-
«Understanding the percentage key helped. »
Did this article help you?
Download Article
Download Article
A percentage is a special way of representing a portion of something. A percentage is a number that indicates a fraction made up of 100 parts. Thus, 100% means the whole thing (whatever is being measured), while 50% means one half. If you learn how to write numbers as percentages, it then becomes easy to perform multiplication and other calculations with percentages on a calculator. Some calculators even have a % button that makes the calculation even easier.[1]
-
1
Review the general meaning of fractions. A fraction is a comparison between two numbers, usually representing the size of a part of something to the size of the whole thing. The classic example is a pie that is cut into eight, for example, equal portions. The top of the fraction, called the
numerator, represents the number of pieces you select.
The bottom of the fraction, called the
denominator, represents the total number of pieces in the pie
— in this case, 8.[2]
- For example, the fraction 1/8 represents one piece of the pie that has been cut in eight pieces.
- The fraction 7/8 represents 7 pieces, almost the full pie.
-
2
Recognize the special relationship of percentages. A percentage is a special kind of fraction in which the
denominator is always set at 100.
[3]
While this is not practical when cutting slices of an actual pie, the concept of percentages is much more useful because it is standard.- With fractions, the size of “half” of something will depend on the number of pieces. If your “pie” is cut into 8 pieces, then half would be 4. But if your “pie” is in 22 pieces, then half would be 11. The target always changes. But with percentages, one-half is always the same — 50%.
- It’s helpful to remember that the word «percent» actually means «of 100″—»per» means «of,» and «cent» means «100.»[4]
Advertisement
-
3
Use a calculator to convert any fraction to a decimal or percentage. If you are presented with any fraction, you can very easily convert it to a decimal number using any calculator. Just recognize that a fraction represents a division problem, and
use your calculator to divide the numerator by the denominator.
Your calculator will give you the decimal equivalent of the fraction.[5]
- Suppose you have the fraction 1/2. On your calculator, perform the operation 1 ÷ 2, and the calculator will show the result 0.5.
- Convert the fraction 1/4 into a decimal by performing the operation 1 ÷ 4. The result is 0.25.
- For a more complicated example, you can convert the fraction 274/312 into a decimal with the operation 274 ÷ 312. The result will be 0.878. (There are more digits, but for our purposes we can stop at three.)
-
4
Convert decimals to percentages by shifting the decimal point. If you have a number that is already represented by a decimal, converting that to a percentage is easy. Because the decimal numbering system is based on factors of 10, you can transform a decimal number into a percentage by simply
shifting the decimal point by two spaces to the right and then adding a % sign.
If your decimal number consists of only one digit, you can add 0’s on the right of the number, such as turning 0.5 into 0.50 or even 0.500. These all have the same numerical value.[6]
- Consider the example above of 1/2, which we converted to the decimal of 0.5. To change this decimal to a percentage, shift the decimal point two spaces to the right. First rewrite 0.5 as 0.50. Then when you shift the decimal point two spaces, you turn 0.50 into the number 50%.
- The example of 1/4, which has a decimal equivalent of 0.25, can be turned into the percentage 25%.
-
5
Memorize basic fraction conversions. It is useful if you can memorize the percentage representations of certain basic fractions. Because the denominator for a percentage is always 100, certain values are constant. Some basic conversions you should know include:[7]
- 3/4 = 75%
- 1/2 = 50%
- 1/3 = 33 1/3%
- 1/4 = 25%
- 1/5 = 20%
- 1/8 = 12.5% (this is often used in banking)
Advertisement
-
1
Add percentages very directly. Because percentages all represent fractions with the common denominator of 100, you can add a list of percentages without any additional work. By contrast, remember that to add fractions, you must work through the steps of finding common denominators and converting your fractions to those common denominators. With percentages, however, no additional work is necessary.[8]
Just add the numbers together.
- If each of six people draws a portion of the company’s payroll, you can find out how much they represent together by just adding the relative percentages. If their respective shares are 10%, 5%, 8%, 22%, 10% and 8%, you can just add 10+5+8+22+10+8 = 63. Those six people make up 63% of the company’s payroll.
- When you are adding, ignore the percent symbol, and just add the numbers. Put the symbol back in your final answer.
-
2
Subtract percentages in the same manner. Again, because percentages represent fractions with the common denominator of 100, you do not need to do any additional work to subtract percentages. If you are working the the concept of removing some percentage from an original whole item, you should represent the whole item with the number 100 (because the whole means 100%).[9]
- Suppose you want to calculate an income percentage. 100% represents the entire income from some project, but then you must subtract, for example, 10% for expenses, 12% for salaries, and 25% for taxes. How much is left? Simply use your calculator to perform the subtraction of 100-10-12-25. The result is 53%.
-
3
Multiply or divide using decimal equivalents. If you have a problem that is initially written as 25% x 30, just
write the 25% as its decimal equivalent 0.25 and conduct the operation.
This would be 0.25 x 30 which gives the result of 7.5.[10]
Similarly, if you have a division problem of 200 ÷ 10%, rewrite this as 200 ÷ 0.10 and enter this into your calculator. You will get the result of 2000.[11]
- The last result may appear surprising, if you expect division to produce a smaller result than the starting number. However, you should understand that division by a number less than one will always lead to an increase by the reciprocal of that number. For example,
dividing by 1/10 is the same as multiplying by 10.
Dividing by 1/2 is the same as multiplying by 2.
- The last result may appear surprising, if you expect division to produce a smaller result than the starting number. However, you should understand that division by a number less than one will always lead to an increase by the reciprocal of that number. For example,
Advertisement
-
1
Perform multiplication to find the percent “of” a number. A common calculation involving percentages is to find some percent “of” another number. For example, if you are in a restaurant you may want to tip 15% “of” your total bill. When working with percentages,
the word “of” carries the same meaning as “times” or “multiply.”
Therefore, 15% “of” 100, for example, means the same as 15% x 100.[12]
-
2
Convert the percentage to a decimal and multiply. To calculate the percentage of the whole number, you need to first turn the percentage into a decimal as already described. Then simply multiply.[13]
- To find 15% of 100, rewrite the 15% as 0.15. Then just multiply 0.15 x 100, to get the solution of 15.
-
3
Write your result without a percentage symbol. When you set out to find a percentage of a whole number,
your result will be a number and not a percentage.
You may begin with a percentage symbol, but when you convert that percentage to a decimal to conduct the multiplication, your answer will no longer have a percentage symbol.[14]
- In the example of 15% of 100, the result is the whole number 15.
Advertisement
-
1
Find the % key on your calculator. Most simple calculators will contain a key with the % symbol. More advanced, graphing calculators may not have this key because the makers expect that you can operate without it. But many more basic calculators will have it.[15]
-
2
Experiment with the % key for decimal conversions. The simplest use of the % key is to
convert any number from its percentage form to its decimal form.
Just enter the number and press the % button, and the calculator will show the decimal equivalent.
- To represent the number 4% on your calculator, just press the button 4 and then %. Your calculator will turn the number 4 into 0.04, which is the decimal equivalent.
- To change the number 82.5% into a decimal, just type the buttons 8, 2, . , 5, %. The calculator will now show the value of 0.825.
-
3
Use the % key for calculations. The % key on your calculator makes certain calculations very simple. Suppose you want to calculate a tip amount, and you want to find 15% of the total bill of $75.32. If you have your calculator available, you will enter the buttons 15% x 75.32. You should get the result of 11.298, which represents a tip of $11.30.[16]
- Whenever you are using a calculator for percentage calculations, you should make sure to press the Clear (C) or All Clear (AC) button before starting.
- As you enter the numbers for this calculation, you should notice that as soon as your hit the % button, your number of 15 converts to .15. The calculator will the proceed to calculate .15 x 75.32.
Advertisement
Add New Question
-
Question
How do you easily add the tip to a bill at a restaurant?
David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Academic Tutor
Expert Answer
Support wikiHow by
unlocking this expert answer.You can easily calculate your total bill including a tip or a tax by adding 1 to the percentage. For example, if you have a $20 meal and you want to add 15% to the bill, multiply $20 by 1.15 to get $23. That’s faster than figuring out 15% of $20, which is $3, then adding it back to $20.
-
Question
How do you take a percent of a number that isn’t 100?
David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
Academic Tutor
Expert Answer
Support wikiHow by
unlocking this expert answer.If you have a problem like «What’s 25% of 50?» turn the percent into a decimal. In this case, 25% is the same as 0.25. Then, you’d multiply that by the second number—0.25 times 50, which is 12.5.
-
Question
What is 6% off 299.00?
Multiply 299.00 by 0.06 to get the amount of the discount. Subtract that amount from 299.00 to find the number that replaces 299.00.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Things You’ll Need
- Calculator
- Pencil
- Paper
References
About This Article
Article SummaryX
To do percentages on a calculator using the percentage button, enter the percentage times the original number. For example, if you wanted to give a waiter a 20% tip on your $50 order, you would enter 20 and hit the percentage button to get 20%. Then you would hit the multiplication button, enter 50, and hit the equals button to find that 20% of $50 is $10. Read more to learn how to find percentages without using the percentage button!
Did this summary help you?
Thanks to all authors for creating a page that has been read 452,740 times.
Reader Success Stories
-
«Understanding the percentage key helped. »
Did this article help you?
Доброго времени суток!
Проценты, скажу я вам, это не только что-то «скучное» на уроках математики в школе, но еще и архи-нужная и прикладная вещь в жизни 👌 (встречаемая повсюду: когда берете кредит, оцениваете скидку, считаете прибыль и т.д.).
И на мой взгляд, при изучении темы «процентов» в той же школе — этому уделяется чрезвычайно мало времени. Возможно, из-за этого, некоторые люди попадают в не очень приятные ситуации (многие из которых можно было бы избежать, если бы вовремя прикинуть что там и как…).
Собственно, в этой статье хочу разобрать наиболее популярные задачи с процентами, которые как раз встречаются в жизни (разумеется, рассмотрю это как можно на более простом языке с примерами). Ну а предупрежден — значит вооружен 😉 (думаю, что знание этой темы позволит многим сэкономить и время, и деньги).
Итак, ближе к теме…
*
Содержание статьи
- 1 Как посчитать проценты: примеры
- 1.1 Вариант 1: расчет простых чисел в уме за 2-3 сек.
- 1.2 Вариант 2: используем калькулятор телефона на Андроид
- 1.3 Вариант 3: считаем процент от числа (суть расчета + золотое правило)
- 1.4 Вариант 4: считаем проценты в Excel
→ Задать вопрос | дополнить
Как посчитать проценты: примеры
Вариант 1: расчет простых чисел в уме за 2-3 сек.
В подавляющем большинстве случаев в жизни требуется быстро прикинуть в уме, сколько там это будет скидка в 10% от какого-то числа (например). Согласитесь, чтобы принять решение о покупке, вам ненужно высчитывать все вплоть до копейки (важно прикинуть порядок).
Наиболее распространенные варианты чисел с процентами привел в списке ниже, а также, на что нужно разделить число, чтобы узнать искомую величину.
Простые примеры:
- 1% от числа = разделить число на 100 (1% от 200 = 200/100 = 2);
- 10% от числа = разделить число на 10 (10% от 200 = 200/10 = 20);
- 25% от числа = разделить число на 4 или два раза на 2 (25% от 200 = 200/4 = 50);
- 33% от числа ≈ разделить число на 3;
- 50% от числа = разделить число на 2.
Задачка! Например, вы хотите купить технику за 197 тыс. руб. Магазин делает скидку в 10,99%, если вы выполняете какие-нибудь условия. Как это быстро прикинуть, стоит ли оно того?
Пример решения. Да просто округлить эти пару чисел: вместо 197 взять сумму в 200, вместо 10,99% взять 10% (условно). Итого, нужно-то 200 разделить на 10 — т.е. мы оценили размер скидки, примерно в 20 тыс. руб. (при определенном опыте расчет делается практически на автомате за 2-3 сек.).
Точный расчет: 197*10,99/100 = 21,65 тыс. руб.
Диаграмма с процентами / в качестве примера
*
Вариант 2: используем калькулятор телефона на Андроид
Когда результат нужен более точный, можно воспользоваться калькулятором на телефоне (в статье ниже приведу скрины с Андроида). Пользоваться им достаточно просто.
Например, вам нужно найти 30% от числа 900. Как это сделать?
Да достаточно легко:
- открыть калькулятор;
- написать 30%900 (естественно, процент и число может быть отличными);
- обратите внимание, что внизу под вашим написанным «уравнением» вы увидите число 270 — это и есть 30% от 900.
30% от числа 900 (калькулятор Андроид)
Ниже представлен более сложный пример. Нашли 17,39% от числа 393 675 (результат 68460,08).
еще один пример
Если вам нужно, например, от 30 000 отнять 10% и узнать сколько это будет, то вы можете так это и написать (кстати, 10% от 30 000 — это 3000).
Таким образом, если от 30 000 отнять 3000 — будет 27000 (что и показал калькулятор). 👇
От числа отнимаем 10% (еще один пример)
В общем-то, весьма удобный инструмент, когда нужно просчитать 2-3 числа и получить точные результаты, вплоть до десятых/сотых.
*
Вариант 3: считаем процент от числа (суть расчета + золотое правило)
Не всегда и не везде можно округлять числа и высчитывать проценты в уме. Причем, иногда требуется не только получить какой-то точный результат, но и понять саму «суть расчета» (например, чтобы просчитать сотню/тысячу различных задачек в Excel).
В этих случаях рекомендую запомнить одно «золотое» правило столбика. Если вы поймете его — то без проблем сможете всегда решать задачки с процентами.
Итак…
Допустим нам необходимо найти 17,39% от числа 393 675. Решим эту простую задачку…
- сначала запишите на листочке число 393675 и напротив него напишите 100% (т.е. число, от которого мы пытаемся найти какой-то процент — считаем за 100%);
- далее под 100% напишите, тот процент, который хотите найти (т.е. 17,39 в нашем примере); под самим числом — поставьте «X» (т.е. то число, что нужно найти, см. скрин ниже). Здесь главное число писать под числом, проценты под процентами (и не путать между собой их)!
Записываем числа для расчета процентов
- теперь смотрите как легко можно найти X: достаточно перемножить между собой исходное число с искомым процентом (правило диагонали: где известны два числа — их перемножаем) и разделить на 100. См. скрин ниже. Перемножить можно на калькуляторе (делов-то на 10-15 сек.).
Крест на крест (считаем проценты)
Чтобы снять все точки на «Й», рассмотрю обратную задачу. Например, сколько процентов составляет число 30 000 от числа 393 675.
- сначала записываем столбиком также 393 675 и напротив него ставим 100%;
- далее под самим числом 393 675 пишем 30 000, а напротив него ставим X (т.е. то, что нам нужно найти);
- далее (30 000 * 100)/393675 и получаем 7,62 % (можете проверить 👌). Т.е. работает тоже правило: перемножаем крест на крест (т.е. там, где в диагонали известны два числа) и делим на оставшееся. Таким образом легко найти неизвестное.
Обратная задачка с процентами
*
Вариант 4: считаем проценты в Excel
Excel хорош тем, что позволяет производить достаточно объемные расчеты: можно одновременно просчитывать десятки самых различных таблиц, связав их между собой. Да и вообще, разве вручную просчитаешь проценты для десятков наименований товаров, например.
Ниже покажу парочку примеров, с которыми наиболее часто приходится сталкиваться.
Задачка первая. Есть два числа, например, цена покупки и продажи. Надо узнать разницу между этими двумя числами в процентах (насколько одно больше/меньше другого).
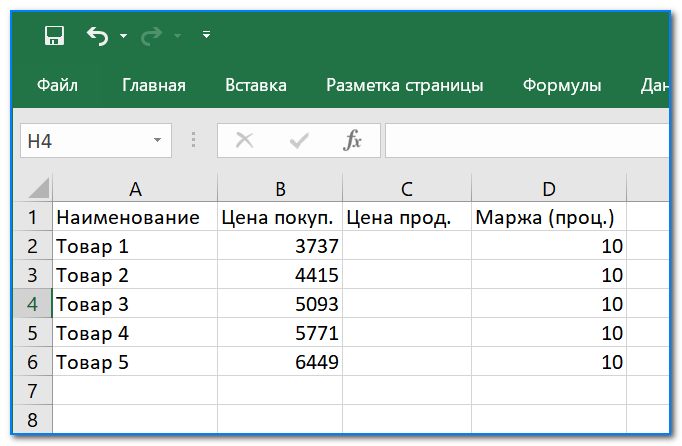
- Сначала оформляем все это в Excel в форме таблички (пример см. ниже: в моем случае будем считать проценты для столбика «Маржа» по цене покупки и цене продажи товара);
Как определить, насколько одно число больше другого в процентах
- далее на всякий случай напомню, как узнать сколько процентов составляет одно число от другого (для примера взял первую сточку из таблицы выше). Согласно простому «правилу» (о нем рассказывал чуть ранее в статье) получаем, что разница между этими числами 4,36%. См. скрин ниже.
Второе число составляет 104% от первого
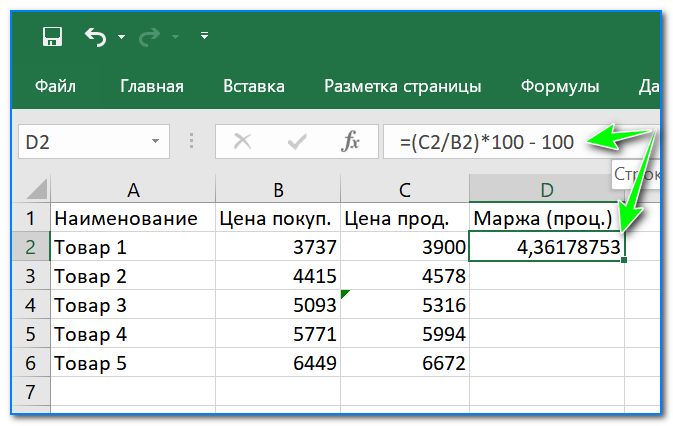
- теперь осталось записать эту формулу в Excel: =(C2/B2)*100 — 100 (см. скрин ниже). Задачка для первой строки решена — разница между ценой покупки и ценой продажи 4,36%.
Пишем формулу
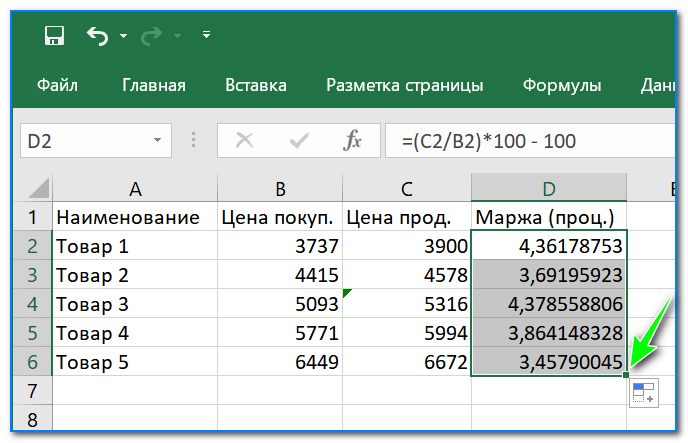
- для того, чтобы просчитать проценты для всех остальных строк — достаточно растянуть формулу (см. скрин ниже 👇).
Формулу растянули — проценты посчитаны для всего столбца
Для более точного понимания, приведу еще один пример. Другая задачка: есть цена покупки и желаемый процент прибыли (допустим 10%). Как узнать цену продажи. Вроде бы все просто, но многие «спотыкаются»…
- сначала также открываем Excel и заносим данные в табличку;
За какую цену продавать, если нужна маржа в 10%
- далее нам нужно найти 10% от цены покупки (т.е. то число, на которое нужно увеличить цену покупки). Чтобы это сделать для первой строки таблицы, все по тому же правилу (см. скрин ниже 👇) нужно: (3737*10)/100 = 373,7
Считаем, насколько одно число больше другого в процентах
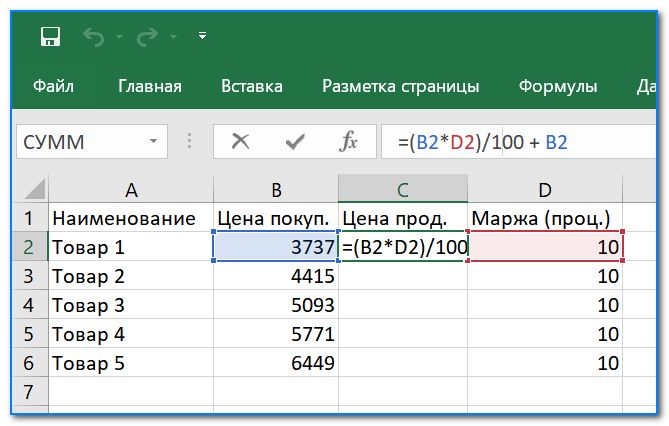
- Теперь можно оформить формулу для первой строки в Excel: =(B2*D2)/100 + B2 (см. скрин ниже 👇). Т.е. сначала мы нашли сколько будет 10% от цены покупки, а затем прибавили к этому числу цену покупки. Вроде бы все просто и логично 👌.
Пишем формулу для нашей задачи
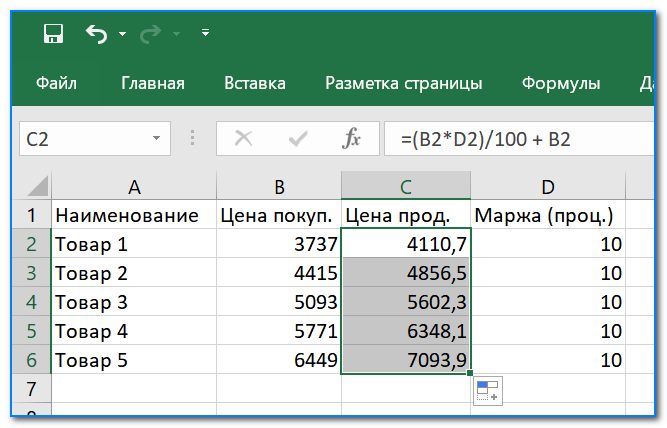
- ну и последний штрих: просто растягиваем формулу на остальные строки. Задачка решена!
Растягиваем формулу — задача решена
*
Комментарии по теме — всегда приветствуются…
На этом всё, удачи!
👋
Первая публикация: 14.10.2018
Корректировка: 23.10.2022

Полезный софт:
-
- Видео-Монтаж
Отличное ПО для создания своих первых видеороликов (все действия идут по шагам!).
Видео сделает даже новичок!
-
- Ускоритель компьютера
Программа для очистки Windows от «мусора» (удаляет временные файлы, ускоряет систему, оптимизирует реестр).