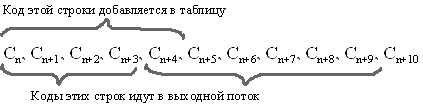Применение алгоритмов кодирования в архиваторах для обеспечения продуктивной работы в windows

Другие методы кодирования

Мы
рассмотрели лишь несколько наиболее
известных алгоритмов сжатия данных,
дабы дать читателям поверхностное
представление о методах сжатия данных.
Конечно же, самих алгоритмов сжатия
разработано очень много, и их рассмотрение
не входит в задачи данной публикации.
Тем не менее при рассмотрении архиваторов
WinRAR, WinZip и 7-Zip можно встретить упоминание
о таких алгоритмах кодирования, как
PPMd, LZMA и bzip2. А потому вкратце поясним, о
чем идет речь.

Итак,
начнем с метода PPM (PPMd — это одна из
многочисленных вариаций метода PPM).

PPM
(Prediction by Partial Matching) — это алгоритм
сжатия данных без потерь, основанный
на контекстном моделировании и
предсказании (предсказание по частичному
совпадению).

Метод
PPM был предложен еще в 1984 году Клири
(Cleary) и Уиттеном (Witten) и до настоящего
времени широко используется, поскольку
является одним из наиболее эффективных
методов экономного кодирования.

В
рассмотренных нами ранее методах для
кодирования информационных сообщений
требовалось знание вероятности появления
символов. В случае если нет никакой
дополнительной информации об источнике,
определить эти вероятности можно только
путем статистического анализа его
информационной выборки. Данный принцип
лежит в основе статистических методов
экономного кодирования, к которым
относится и метод PPM.

В
модели PPM используется понятие так
называемого контекста, под которым
понимается множество символов в несжатом
потоке, предшествующих данному. На
основе статистики, собираемой в процессе
обработки информации, статистический
метод позволяет оценить вероятность
появления в текущем контексте произвольного
символа или последовательности символов.

Длина
контекста, применяемого при предсказании,
обычно очень ограниченна. Эта длина
обозначается N и называется порядком
контекста, или порядком модели PPM. Если
предсказание символа по контексту из
N символов не может быть произведено,
то предпринимается попытка предсказать
его с помощью контекста более низкого
порядка. Рекурсивный переход к моделям
с меньшим порядком реализуется, пока
предсказание не произойдет в одной из
моделей либо когда контекст приобретет
нулевую длину (N = 0).

Сам
алгоритм PPM лишь предсказывает значение
символа, а непосредственное сжатие
осуществляется такими алгоритмами, как
алгоритм Хаффмана или арифметическое
кодирование.

Отметим,
что алгоритм PPM имеет множество вариаций
и используется, в частности, в архиваторах
WinRAR (алгоритмы PPMd и PPMII), 7-Zip (алгоритм
PPMd) и WinZip (алгоритм PPMd).

Еще
один часто применяемый алгоритм сжатия —
это LZMA (Lempel-Ziv-Markov chain-Algorithm), который был
разработан в 2001 году и является
своеобразным вариантом алгоритма LZW. В
этом алгоритме используется метод
скользящего окна и интервального
кодирования.

Алгоритм
LZMA находит применение в архиваторах
7-Zip и WinZip.

Последний
алгоритм, о котором мы упомянем, —
это алгоритм bzip2, основанный на
преобразовании Барроуза—Уилера
(Burrows—Wheeler Transform, BWT). В алгоритме bzip2
преобразование BWT используется для
превращения последовательностей
многократно чередующихся символов в
строки одинаковых символов, а затем
применяется преобразование MTF, а в
заключение — кодирование Хаффмана.
Процесс BWT-преобразования очень прост —
он выполняется в три этапа, которые мы
рассмотрим на примере исходной
информационной последовательности
«BANAN».

На
первом этапе составляется таблица всех
циклических сдвигов входной строки. В
нашем случае из строки «BANAN» мы получим
путем циклического сдвига еще четыре
строки: «ANANB», «NANBA», «ANBAN» и «NBANA».

На
следующем этапе производится сортировка
в алфавитном порядке всех полученных
строк, включая исходную (табл.
2).
На последнем этапе мы выписываем строку,
полученную по последним символам (сверху
вниз) всех отсортированных строк. То
есть если все отсортированные строки
представить в виде матрицы, то нужная
нам строка образована последним столбцом
этой матрицы. В нашем случае получим
строку «BNNAA». Кроме того, для возможности
восстановления исходной строки по
преобразованной нам нужно запомнить
еще и номер исходной строки в отсортированном
списке строк. В нашем случае это третья
строка, поэтому результат преобразования
можно записать как BWT = («BNNAA», 3).

Важно,
что в результате BWT-преобразования все
повторяющиеся символы группируются
вместе, что очень удобно для последующего
кодирования.

Теперь
посмотрим, как сделать обратное
преобразование. Итак, мы имеем результат
преобразования в виде «BNNAA», 3.

Сначала
записываем в столбик нашу строку «BNNAA».
Затем сортируем все символы этого
столбца в алфавитном порядке. Далее,
слева от полученного столбца записываем
столбец «BNNAA» и производим сортировку
в алфавитном порядке уже всех двухсимвольных
строк. Далее дописываем к эти двум
столбцам слева опять столбец «BNNAA» и
производим сортировку в алфавитном
порядке уже всех трехсимвольных строк.
Процедуру продолжаем до тех пор, пока
строки не будут содержать по пять
символов. В отсортированной по пяти
символам матрице находим третью строку
(напомним, что номер три мы изначально
запомнили), которая и будет представлять
раскодированную последовательность
символов (табл.
3).

Как
видите, прямое и обратное BWT-преобразование
реализуется очень просто.

Итак,
мы рассмотрели наиболее важные алгоритмы
сжатия информации, которые находят
применение в современных архиваторах.
При этом мы преследовали лишь одну
цель — продемонстрировать, каким
образом можно реализовать сжатие
информации без потерь. Однако мы не
стремились к детальному рассмотрению
всех алгоритмов сжатия информации, тем
более что количество их огромно.

Ну
а теперь давайте познакомимся с тремя
наиболее популярными архиваторами,
реализующими сжатие данных без потерь
с использованием различных алгоритмов.

Тестируемые
архиваторы

WinRAR
4.2

Архиватор
WinRAR — это Windows-версия архиватора RAR.
Он предназначен для создания архивов
в форматах RAR и ZIP. Кроме того, этот
архиватор позволяет распаковывать
архивы форматов 7Z, ACE, ARJ, BZIP2, CAB, GZ, ISO, JAR,
LZH, TAR, UUE, Z.

Существует
32- и 64-разрядная версия WinRAR. В дальнейшем
мы будем рассматривать только 64-битную
версию.

WinRAR
позволяет создавать крупный архив с
дроблением его на части (тома) заданного
размера. Это очень удобно, когда необходимо
передать большой объем данных через
файлообменные серверы в Интернете,
большинство из которых обладают
ограничением по размеру одного
передаваемого файла. Кроме того, можно
использовать архивацию без сжатия,
когда множество файлов и папок объединяются
в один общий файл (архив). Данный способ
часто используется для повышения
скорости копирования, поскольку один
архивный файл будет копироваться гораздо
быстрее, чем множество отдельных файлов.

Среди
функций WinRAR также стоит выделить
возможность создания самораспаковывающихся
SFX-архивов, распаковать которые можно
без всяких архиваторов. Кроме того,
пользуясь WinRAR, можно надежно защитить
содержимое архива от свободного просмотра
и распаковки с помощью пароля.

WinRAR
также имеет встроенную командную строку,
что очень удобно при написании различных
скриптов.

При
архивации WinRAR позволяет выбрать один
из пяти вариантов сжатия (Store, Fastest, Fast,
Normal, Good, Best). Вариант Store подразумевает
отсутствие сжатия, а вариант Best —
максимальную степень сжатия, но и
максимальное время архивации.

Архиватор
WinRAR является платным.

WinZip
17

Архиватор
формата ZIP (PKZIP) был первоначально создан
для MS-DOS в 1989 году компанией PKWare и сегодня
является одним из самых распространенных.
Версия WinZip появилась в 1990-м как коммерческий
графический интерфейс для PKZIP.

В
мае 2006 года корпорация Corel объявила о
приобретении WinZip Computing.

В
конце 2012-го компания WinZip Computing (подразделение
компании Corel) представила новую
русифицированную версию приложения
WinZip 17, которая оптимизирована для
многоядерных процессоров и поддерживает
возможность использования вычислительных
мощностей графических процессоров,
встроенных в процессоры Intel Core третьего
поколения, процессоры AMD A-Series APU, а также
дискретные графические карты AMD Radeon и
NVIDIA GeForce.

Архиватор
WinZip 17 является 64-битным и позволяет
создавать архивы в форматах ZIP и ZIPX, а
также распаковывать архивы форматов
7Z, RAR, BZIP2, LHA/LZH, CAB, ISO и других (каких именно,
в документации не уточняется).

Вообще
архиватор WinZip 17 обладает большим
количеством дополнительных возможности
и функций, но сейчас мы их касаться не
будем, а рассмотрим лишь его возможности
по созданию архивов.

Естественно,
WinZip 17 позволяет создавать архив с
дроблением его на тома заданного размера.
Кроме того, можно использовать архивацию
без сжатия, когда множество файлов и
папок объединяются в один общий файл
(архив).

Кроме
того, поддерживается возможность
шифрования архива (128- и 256-битное
AES-шифрование).

При
архивации WinZip позволяет задать уровень
компрессии и алгоритм сжатия. Для формата
ZIPX можно выбрать алгоритм PPMd, LZMA или
bzip2, которые обеспечивают очень высокую
степень сжатия. Кроме того, имеется
вариант, называемый Best Method, предусматривающий
максимальную степень сжатия. При выборе
данного метода архиватор сам выбирает
оптимальный алгоритм сжатия, обеспечивающий
максимальную степень компрессии, в
зависимости от типа файла.

Также
отметим, что WinZip не имеет встроенной
командной строки, однако в случае ее
необходимости можно скачать дополнение
WinZip Command Line Support Add-On Version 3.2, которое
обеспечивает работу с командной строкой.

Архиватор
WinZip является платным.

7-Zip
9.30

В
отличие от архиваторов WinRAR и WinZip,
архиватор 7-Zip абсолютно бесплатный.
7-Zip — это программное обеспечение с
открытым кодом, при этом большая часть
исходного кода находится под лицензией
GNU LGPL.

Существует
как 32-, так и 64-битная версии этого
архиватора. Текущей версией, появившейся
в конце 2012 года, является версия 9.30.

Архиватор
7-Zip имеет удобный графический интерфейс,
но при этом поддерживает работу с
командной строкой.

Основным
форматом для архиватора 7-Zip является
собственный формат 7Z с компрессией
LZMA. Кроме того, 7-Zip позволяет производить
архивирование/разархивирование в
форматах ZIP, GZIP, BZIP2 и TAR. Также поддерживается
разархивирование форматов ARJ, CAB, CHM,
CPIO, DEB, DMG, HFS, ISO, LZH, LZMA, MSI, NSIS, RAR, RPM, UDF, WIM,
XAR и Z.

Как
утверждает производитель, архиватор
7-Zip обеспечивает степень сжатия выше,
чем RAR, за исключением мультимедийных
данных. Более того, считается, что по
степени сжатия 7-Zip уступает только
архиваторам PAQ и его GUI-модификации KGB,
которые, однако, имеют на порядок большее
время сжатия.

Для
форматов ZIP и GZIP архиватор 7-Zip предлагает
сжатие, которое на 2-10% лучше, чем
предоставляемое архиваторами PKZip и
WinZip

Программа
поддерживает работу на 64-битных
операционных системах. Интерфейс
программы переведен на множество языков,
включая русский.

Отметим,
что архиватор позволяет создавать
самораспаковывающиеся архивы для
формата 7z. Кроме того, поддерживается
шифрование AES 256-бит.

Естественно,
архиватор 7-Zip (как WinZip и WinRAR) интегрируется
в проводник Windows и доступен через
контекстное меню.

Еще
одна особенность заключается в том, что
в архиваторе 7-Zip предусмотрен плагин
для FAR Manager.

Для
своего родного формата 7z архиватор
позволяет выбрать уровень сжатия (без
сжатия, «Скоростной», «Быстрый»,
«Нормальный», «Максимальный», «Ультра»),
а также задать алгоритм сжатия (LZMA2,
LZMA, PPMd, BZip2).

Кроме
того, дополнительно можно задать размер
словаря, размер слова, размер блока и
число потоков.

Также
поддерживается создание архивов,
разбитых на тома заданного размера.

Соседние файлы в папке 1

• #
• #

Методы Шеннона-Фэно, Хаффмена и арифметическое кодирование обобщающе
называются статистическими методами.
Словарные алгоритмы носят более практичный характер.
Их частое преимущество перед статистическими теоретически объясняется тем,
что они позволяют кодировать последовательности символов разной длины.
Неадаптивные статистические алгоритмы тоже можно использовать для таких
последовательностей, но в этом случае их реализация становится весьма
ресурсоемкой.

Алгоритм LZ77 был опубликован в 1977 г.
Разработан израильскими математиками Якобом Зивом (Ziv) и Авраамом Лемпелом (Lempel). Многие
программы сжатия информации используют ту или иную
модификацию LZ77. Одной из причин популярности алгоритмов LZ является их
исключительная простота при высокой эффективности сжатия.

Основная идея LZ77 состоит в том, что второе и последующие
вхождения некоторой строки символов в сообщении заменяются ссылками на
ее первое вхождение.

LZ77 использует уже просмотренную часть сообщения как словарь. Чтобы
добиться сжатия, он пытается заменить очередной фрагмент сообщения на
указатель в содержимое словаря.

LZ77 использует «скользящее» по сообщению окно, разделенное на две
неравные части. Первая, большая по размеру, включает уже просмотренную
часть сообщения. Вторая, намного меньшая, является буфером, содержащим
еще незакодированные символы входного потока. Обычно размер окна составляет
несколько килобайт, а размер буфера — не более ста байт. Алгоритм пытается
найти в словаре (большей части окна) фрагмент, совпадающий с содержимым
буфера.

Алгоритм LZ77 выдает коды, состоящие из трех элементов:

• смещение в словаре относительно его начала подстроки, совпадающей с началом содержимого буфера;
• длина этой подстроки;
• первый символ буфера, следующий за подстрокой.

Пример. Размер окна — 20 символ, словаря — 12 символов, а буфера — 8.
Кодируется сообщение «ПРОГРАММНЫЕ ПРОДУКТЫ ФИРМЫ MICROSOFT».
Пусть словарь уже заполнен. Тогда он содержит строку «ПРОГРАММНЫЕ «,
а буфер — строку «ПРОДУКТЫ».
Просматривая словарь, алгоритм обнаружит, что совпадающей
подстрокой будет «ПРО», в словаре она расположена со смещением 0 и имеет
длину 3 символа, а следующим символом в буфере является «Д». Таким образом,
выходным кодом будет тройка <0,3,’Д’>. После этого алгоритм сдвигает влево
все содержимое окна на длину совпадающей подстроки 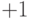и
одновременно
считывает столько же символов из входного потока в буфер. Получаем в словаре
строку «РАММНЫЕ ПРОД», в буфере — «УКТЫ ФИР».
В данной ситуации совпадающей подстроки обнаружить не удаться и алгоритм
выдаст код <0,0,’У’>, после чего сдвинет окно на один символ.
Затем словарь будет содержать «АММНЫЕ ПРОДУ», а буфер — «КТЫ ФИРМ».
И т.д.

Декодирование кодов LZ77 проще их получения, т.к. не нужно
осуществлять поиск в словаре.

Недостатки LZ77:

• с ростом размеров словаря скорость работы алгоритма-кодера
  пропорционально замедляется;
• кодирование одиночных символов очень неэффективно.

Кодирование одиночных символов можно сделать эффективным, отказавшись от
ненужной ссылки на словарь для них. Кроме того, в некоторые модификации
LZ77 для повышения степени сжатия добавляется возможность для кодирования
идущих подряд одинаковых символов.

Пример. Закодировать по алгоритму LZ77 строку «КРАСНАЯ КРАСКА».

В последней строчке, буква «А» берется не из словаря, т.к. она
последняя.

Длина кода вычисляется следующим образом: длина подстроки не может
быть больше размера буфера, а смещение не может быть больше размера
словаря . Следовательно, длина двоичного кода смещения будет
округленным в большую сторону размер словаря , а
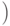
длина двоичного кода для длины подстроки будет округленным в большую
сторону размер буфера . А символ кодируется
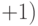
8 битами (например,
ASCII+).

В последнем примере длина полученного кода равна
бит, против 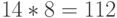бит исходной длины строки.

В 1982 г. Сторером (Storer) и Шиманским (Szimanski) на базе LZ77 был
разработан алгоритм LZSS, который отличается от LZ77 производимыми кодами.

Код, выдаваемый LZSS, начинается с однобитного префикса, различающего
собственно код от незакодированного символа. Код состоит из пары: смещение
и длина, такими же как и для LZ77. В LZSS окно сдвигается ровно на длину
найденной подстроки или на 1, если не найдено вхождение подстроки из буфера в
словарь. Длина подстроки в LZSS всегда больше нуля, поэтому длина двоичного
кода для длины подстроки — это округленный до большего целого двоичный
логарифм от длины буфера.

Пример. Закодировать по алгоритму LZSS строку «КРАСНАЯ КРАСКА».

Здесь длина полученного кода равна 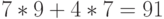бит.

LZ77 и LZSS обладают следующими очевидными недостатками:

1. невозможность кодирования подстрок, отстоящих друг от друга на
   расстоянии, большем длины словаря;
2. длина подстроки, которую можно закодировать, ограничена размером
   буфера.

Хочется продолжить свою предыдущую тему об алгоритмах сжатия. В этот раз я расскажу об алгоритме LZW и немного об его родственниках алгоритмах LZ77 и LZ78.

Алгоритм LZW

Алгоритм Лемпеля — Зива — Велча (Lempel-Ziv-Welch, LZW) — это универсальный алгоритм сжатия данных без потерь.

Непосредственным предшественником LZW явился алгоритм LZ78, опубликованный Абрахамом Лемпелем(Abraham Lempel) и Якобом Зивом (Jacob Ziv) в 1978 г. Этот алгоритм воспринимался как математическая абстракция до 1984 г., когда Терри Уэлч (Terry A. Welch) опубликовал свою работу с модифицированным алгоритмом, получившим в дальнейшем название LZW (Lempel-Ziv-Welch).

Описание

Процесс сжатия выглядит следующим образом. Последовательно считываются символы входного потока и происходит проверка, существует ли в созданной таблице строк такая строка. Если такая строка существует, считывается следующий символ, а если строка не существует, в поток заносится код для предыдущей найденной строки, строка заносится в таблицу, а поиск начинается снова.
Например, если сжимают байтовые данные (текст), то строк в таблице окажется 256 (от «0» до «255»). Если используется 10-битный код, то под коды для строк остаются значения в диапазоне от 256 до 1023. Новые строки формируют таблицу последовательно, т. е. можно считать индекс строки ее кодом.
Алгоритму декодирования на входе требуется только закодированный текст, поскольку он может воссоздать соответствующую таблицу преобразования непосредственно по закодированному тексту. Алгоритм генерирует однозначно декодируемый код за счет того, что каждый раз, когда генерируется новый код, новая строка добавляется в таблицу строк. LZW постоянно проверяет, является ли строка уже известной, и, если так, выводит существующий код без генерации нового. Таким образом, каждая строка будет храниться в единственном экземпляре и иметь свой уникальный номер. Следовательно, при дешифровании при получении нового кода генерируется новая строка, а при получении уже известного, строка ивлекается из словаря.

Псевдокод алгоритма

1. Инициализация словаря всеми возможными односимвольными фразами. Инициализация входной фразы ω первым символом сообщения.
2. Считать очередной символ K из кодируемого сообщения.
3. Если КОНЕЦ_СООБЩЕНИЯ, то выдать код для ω, иначе:
4. Если фраза ω(K) уже есть в словаре, присвоить входной фразе значение ω(K) и перейти к Шагу 2, иначе выдать код ω, добавить ω(K) в словарь, присвоить входной фразе значение K и перейти к Шагу 2.
5. Конец

Пример

Просто по псевдокоду понять работу алгоритма не очень легко, поэтому рассмотрим Рассмотрим пример сжатия и декодирования изображения.
Сначала создадим начальный словарь единичных символов. В стандартной кодировке ASCII имеется 256 различных символов, поэтому, для того, чтобы все они были корректно закодированы (если нам неизвестно, какие символы будут присутствовать в исходном файле, а какие — нет), начальный размер кода будет равен 8 битам. Если нам заранее известно, что в исходном файле будет меньшее количество различных символов, то вполне разумно уменьшить количество бит. Чтобы инициализировать таблицу, мы установим соответствие кода 0 соответствующему символу с битовым кодом 00000000, тогда 1 соответствует символу с кодом 00000001, и т.д., до кода 255. На самом деле мы указали, что каждый код от 0 до 255 является корневым.
Больше в таблице не будет других кодов, обладающих этим свойством.
По мере роста словаря, размер групп должен расти, с тем, чтобы учесть новые элементы. 8-битные группы дают 256 возможных комбинации бит, поэтому, когда в словаре появится 256-е слово, алгоритм должен перейти к 9-битным группам. При появлении 512-ого слова произойдет переход к 10-битным группам, что дает возможность запоминать уже 1024 слова и т.д.
В нашем примере алгоритму заранее известно о том, что будет использоваться всего 5 различных символов, следовательно, для их хранения будет использоваться минимальное количество бит, позволяющее нам их запомнить, то есть 3 ( 8 различных комбинаций ).

Кодирование

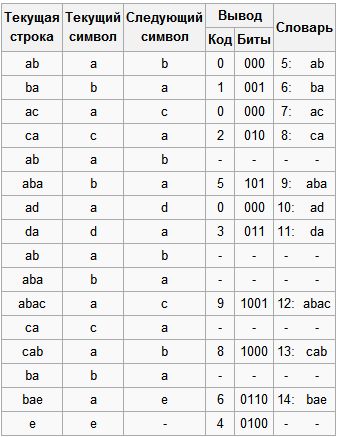
Пусть мы сжимаем последовательность «abacabadabacabae».

• Шаг 1: Тогда, согласно изложенному выше алгоритму, мы добавим к изначально пустой строке “a” и проверим, есть ли строка “a” в таблице. Поскольку мы при инициализации занесли в таблицу все строки из одного символа, то строка “a” есть в таблице.
• Шаг 2: Далее мы читаем следующий символ «b» из входного потока и проверяем, есть ли строка “ab” в таблице. Такой строки в таблице пока нет.
• Добавляем в таблицу <5> “ab”. В поток: <0>;
• Шаг 3: “ba” — нет. В таблицу: <6> “ba”. В поток: <1>;
• Шаг 4: “ac” — нет. В таблицу: <7> “ac”. В поток: <0>;
• Шаг 5: “ca” — нет. В таблицу: <8> “ca”. В поток: <2>;
• Шаг 6: “ab” — есть в таблице; “aba” — нет. В таблицу: <9> “aba”. В поток: <5>;
• Шаг 7: “ad” — нет. В таблицу: <10> “ad”. В поток: <0>;
• Шаг 8: “da” — нет. В таблицу: <11> “da”. В поток: <3>;
• Шаг 9: “aba” — есть в таблице; “abac” — нет. В таблицу: <12> “abac”. В поток: <9>;
• Шаг 10: “ca” — есть в таблице; “cab” — нет. В таблицу: <13> “cab”. В поток: <8>;
• Шаг 11: “ba” — есть в таблице; “bae” — нет. В таблицу: <14> “bae”. В поток: <6>;
• Шаг 12: И, наконец последняя строка “e”, за ней идет конец сообщения, поэтому мы просто выводим в поток <4>.

Итак, мы получаем закодированное сообщение «0 1 0 2 5 0 3 9 8 6 4», что на 11 бит короче.

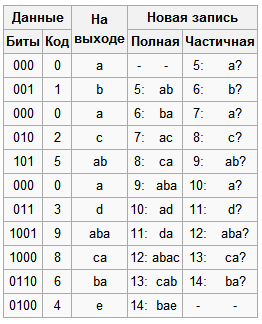
Декодирование

Особенность LZW заключается в том, что для декомпрессии нам не надо сохранять таблицу строк в файл для распаковки. Алгоритм построен таким образом, что мы в состоянии восстановить таблицу строк, пользуясь только потоком кодов.
Теперь представим, что мы получили закодированное сообщение, приведённое выше, и нам нужно его декодировать. Прежде всего, нам нужно знать начальный словарь, а последующие записи словаря мы можем реконструировать уже на ходу, поскольку они являются просто конкатенацией предыдущих записей.

Дополнение

Для повышения степени сжатия изображений данным методом часто используется одна «хитрость» реализации этого алгоритма. Некоторые файлы, подвергаемые сжатию с помощью LZW, имеют часто встречающиеся цепочки одинаковых символов, например aaaaaa … или 30, 30, 30 … и т. п. Их непосредственное сжатие будет генерировать выходной код 0, 0, 5 и т.д. Спрашивается, можно ли в этом частном случае повысить степень сжатия?
Оказывается, это возможно, если оговорить некоторые действия:
Мы знаем, что для каждого кода надо добавлять в таблицу строку, состоящую из уже присутствующей там строки и символа, с которого начинается следующая строка в потоке.

• Итак, кодировщик заносит первую «а» в строку, ищет и находит «а» в словаре. Добавляет в строку следующую «а», находит, что «аа» нет в словаре. Тогда он добавляет запись <5>: «аа» в словарь и выводит метку <0> («а») в выходной поток.
• Далее строка инициализируется второй «а», то есть принимает вид «a?» вводится третья «а», строка вновь равна «аа», которая теперь имеется в словаре.
• Если появляется четвертая «а», то строка «aa?» равна «ааа», которой нет в словаре. Словарь пополняется этой строкой, а на выход идет метка <5> («aa»).
• После этого строка инициализируется третьей «а», и т.д. и т.п. Дальнейший процесс вполне ясен.
• В результате на выходе получаем последовательность 0, 5, 6 …, которая короче прямого кодирования стандартным методом LZW.

Можно показать, что такая последовательность будет корректно восстановлена. Декодировщик сначала читает первый код – это <0>, которому соответствует символ «a». Затем читает код <5>, но этого кода в его таблице нет. Но мы уже знаем, что такая ситуация возможна только в том случае, когда добавляемый символ равен первому символу только что считанной последовательности, то есть «a». Поэтому он добавит в свою таблицу строку «aa» с кодом <5>, а в выходной поток поместит «aa». И так может быть раскодирована вся цепочка кодов.
Мало того, описанное выше правило кодирования мы можем применять в общем случае не только к подряд идущим одинаковым символам, но и к последовательностям, у которых очередной добавляемый символ равен первому символу цепочки.

Достоинства и недостатки

+ Не требует вычисления вероятностей встречаемости символов или кодов.
+ Для декомпрессии не надо сохранять таблицу строк в файл для распаковки. Алгоритм построен таким образом, что мы в состоянии восстановить таблицу строк, пользуясь только потоком кодов.
+ Данный тип компрессии не вносит искажений в исходный графический файл, и подходит для сжатия растровых данных любого типа.
— Алгоритм не проводит анализ входных данных поэтому не оптимален.

Применение

Опубликование алгоритма LZW произвело большое впечатление на всех специалистов по сжатию информации. За этим последовало большое количество программ и приложений с различными вариантами этого метода.
Этот метод позволяет достичь одну из наилучших степеней сжатия среди других существующих методов сжатия графических данных, при полном отсутствии потерь или искажений в исходных файлах. В настоящее время испольуется в файлах формата TIFF, PDF, GIF, PostScript и других, а также отчасти во многих популярных программах сжатия данных (ZIP, ARJ, LHA).

Алгоритмы LZ77 и LZ78

LZ77 и LZ78 — алгоритмы сжатия без потерь, опубликованные в статьях Абрахама Лемпеля и Якоба Зива в 1977 и 1978 годах. Эти алгоритмы наиболее известны в семействе LZ*, которое включает в себя также LZW, LZSS, LZMA и другие алгоритмы. Оба алгоритма относятся к алгоритмам со словарным подходом. LZ77 использует, так называемое, «скользящее окно», что эквивалентно неявному использованию словарного подхода, впервые предложенного в LZ78.

Принцип работы LZ77

Основная идея алгоритма это замена повторного вхождения строки ссылкой на одну из предыдущих позиций вхождения. Для этого используют метод скользящего окна. Скользящее окно можно представить в виде динамической структуры данных, которая организована так, чтобы запоминать «сказанную» ранее информацию и предоставлять к ней доступ. Таким образом, сам процесс сжимающего кодирования согласно LZ77 напоминает написание программы, команды которой позволяют обращаться к элементам скользящего окна, и вместо значений сжимаемой последовательности вставлять ссылки на эти значения в скользящем окне. В стандартном алгоритме LZ77 совпадения строки кодируются парой:

• длина совпадения (match length)
• смещение (offset) или дистанция (distance)

Кодируемая пара трактуется именно как команда копирования символов из скользящего окна с определенной позиции, или дословно как: «Вернуться в словаре на значение смещения символов и скопировать значение длины символов, начиная с текущей позиции». Особенность данного алгоритма сжатия заключается в том, что использование кодируемой пары длина-смещение является не только приемлемым, но и эффективным в тех случаях, когда значение длины превышает значение смещения. Пример с командой копирования не совсем очевиден: «Вернуться на 1 символ назад в буфере и скопировать 7 символов, начиная с текущей позиции». Каким образом можно скопировать 7 символов из буфера, когда в настоящий момент в буфере находится только 1 символ? Однако следующая интерпретация кодирующей пары может прояснить ситуацию: каждые 7 последующих символов совпадают (эквивалентны) с 1 символом перед ними. Это означает, что каждый символ можно однозначно определить переместившись назад в буфере, даже если данный символ еще отсутствует в буфере на момент декодирования текущей пары длина-смещение.

Описание алгоритма

LZ77 использует скользящее по сообщению окно. Допустим, на текущей итерации окно зафиксировано. С правой стороны окна наращиваем подстроку, пока она есть в строке <скользящее окно + наращиваемая строка> и начинается в скользящем окне. Назовем наращиваемую строку буфером. После наращивания алгоритм выдает код состоящий из трех элементов:

• смещение в окне;
• длина буфера;
• последний символ буфера.

В конце итерации алгоритм сдвигает окно на длину равную длине буфера+1.

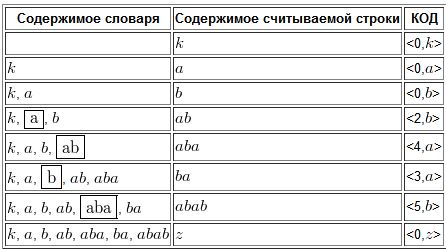
Пример kabababababz

Описание алгоритма LZ78

В отличие от LZ77, работающего с уже полученными данными, LZ78 ориентируется на данные, которые только будут получены (LZ78 не использует скользящее окно, он хранит словарь из уже просмотренных фраз). Алгоритм считывает символы сообщения до тех пор, пока накапливаемая подстрока входит целиком в одну из фраз словаря. Как только эта строка перестанет соответствовать хотя бы одной фразе словаря, алгоритм генерирует код, состоящий из индекса строки в словаре, которая до последнего введенного символа содержала входную строку, и символа, нарушившего совпадение. Затем в словарь добавляется введенная подстрока. Если словарь уже заполнен, то из него предварительно удаляют менее всех используемую в сравнениях фразу. Если в конце алгоритма мы не находим символ, нарушивший совпадения, то тогда мы выдаем код в виде (индекс строки в словаре без последнего символа, последний символ).

Пример kabababababz

и упорядочивать, если необходимо, полученное таким образом дерево.

Процесс работы адаптивного алгоритма Хаффмена с упорядоченным деревом можно изобразить следующей схемой:

Упражнение 26 Закодировать сообщение BBCBBC, используя адаптивный алгоритм Хаффмена с упорядоченным деревом.

Упражнение 27 Закодировать сообщения «AABCDAACCCCDBB», «КИБЕРНЕТИКИ» и «СИНЯЯ СИНЕВА СИНИ», используя адаптивный алгоритм Хаффмена с упорядоченным деревом. Вычислить длины в битах исходного сообщения в коде ASCII+ и его полученного кода.

Упражнение 28 Распаковать сообщение ‘A’0’F’00’X’0111110101011011110100101, полученное по адаптивному алгоритму Хаффмена с упорядоченным деревом, рассчитать длину кода сжатого и несжатого сообщения в битах.
^
Для арифметического кодирования, как и для кодирования методом Хаффмена, существуют адаптивные алгоритмы. Реализация одного из них запатентована фирмой IBM.

Построение арифметического кода для последовательности символов из заданного множества можно реализовать следующим алгоритмом. Каждому символу сопоставляется его вес: вначале он для всех равен 1. Все символы располагаются в естественном порядке, например, по возрастанию. Вероятность каждого символа устанавливается равной его весу, деленному на суммарный вес всех символов. После получения очередного символа и постройки интервала для него, вес этого символа увеличивается на 1 (можно увеличивать вес любым регулярным способом).

Рис. 5.4.

Заданное множество символов — это, как правило, ASCII+. Для того, чтобы обеспечить остановку алгоритма распаковки вначале сжимаемого сообщения надо поставить его длину или ввести дополнительный символ-маркер конца сообщения. Если знать формат файла для сжатия, то вместо начального равномерного распределения весов можно выбрать распределение с учетом этих знаний. Например, в текстовом файле недопустимы ряд управляющих символов и их вес можно занулить.

Пример. Пусть заданное множество — это символы A, B, C. Сжимаемое сообщение — ACCBCAAABC. Введем маркер конца сообщения — E. Кодирование согласно приведенному алгоритму можно провести согласно схеме, приведенной на

рис. 5.4.

Вследствие того, что

Поэтому L₁(ACCBCAAABC)=2.2 бит/сим. Результат, полученный адаптивным алгоритмом Хаффмена — 4.1 бит/сим, но если кодировать буквы не 8 битами, а 2, то результат будет 2.3 бит/сим. В первой строчке схемы выписаны суммарные веса символов, а во второй — длины текущих отрезков.

Способ распаковки адаптивного арифметического кода почти аналогичен приведенному для неадаптивного. Отличие только в том, что на втором шаге после получения нового кода нужно перестроить разбиение единичного отрезка согласно новому распределению весов символов. Получение маркера конца или заданного началом сообщения числа символов означает окончание работы.

Пример. Распакуем код 0010111001010011101101, зная, что множество символов сообщения состоит из A, B, C и E, причем последний — это маркер конца сообщения.

Упражнение 29 Составить адаптивный арифметический код с маркером конца для сообщения BAABC.

^

История происхождения, положительные и отрицательные стороны, сравнение и применение на практике таких алгоритмов, как: LZ77, LZ78, LZSS, LZW. Практические задания для укрепления основного материала лекции. Особенности программ архиваторов. Непосредственное применение алгоритмов кодирования в архиваторах для обеспечения продуктивной работы в MS-DOS и WINDOWS

Методы Шеннона-Фэно, Хаффмена и арифметическое кодирование обобщающе называются статистическими методами. Словарные алгоритмы носят более практичный характер. Их частое преимущество перед статистическими теоретически объясняется тем, что они позволяют кодировать последовательности символов разной длины. Неадаптивные статистические алгоритмы тоже можно использовать для таких последовательностей, но в этом случае их реализация становится весьма ресурсоемкой.

Алгоритм LZ77 был опубликован в 1977 г. Разработан израильскими математиками Якобом Зивом (Ziv) и Авраамом Лемпелом (Lempel). Многие программы сжатия информации используют ту или иную модификацию LZ77. Одной из причин популярности алгоритмов LZ является их исключительная простота при высокой эффективности сжатия.

Основная идея LZ77 состоит в том, что второе и последующие вхождения некоторой строки символов в сообщении заменяются ссылками на ее первое вхождение.

LZ77 использует уже просмотренную часть сообщения как словарь. Чтобы добиться сжатия, он пытается заменить очередной фрагмент сообщения на указатель в содержимое словаря.

LZ77 использует «скользящее» по сообщению окно, разделенное на две неравные части. Первая, большая по размеру, включает уже просмотренную часть сообщения. Вторая, намного меньшая, является буфером, содержащим еще незакодированные символы входного потока. Обычно размер окна составляет несколько килобайт, а размер буфера — не более ста байт. Алгоритм пытается найти в словаре (большей части окна) фрагмент, совпадающий с содержимым буфера.

Алгоритм LZ77 выдает коды, состоящие из трех элементов:

• смещение в словаре относительно его начала подстроки, совпадающей с началом содержимого буфера;
• длина этой подстроки;
• первый символ буфера, следующий за подстрокой.

Пример. Размер окна — 20 символ, словаря — 12 символов, а буфера — 8. Кодируется сообщение «ПРОГРАММНЫЕ ПРОДУКТЫ ФИРМЫ MICROSOFT». Пусть словарь уже заполнен. Тогда он содержит строку «ПРОГРАММНЫЕ «, а буфер — строку «ПРОДУКТЫ». Просматривая словарь, алгоритм обнаружит, что совпадающей подстрокой будет «ПРО», в словаре она расположена со смещением 0 и имеет длину 3 символа, а следующим символом в буфере является «Д». Таким образом, выходным кодом будет тройка <0,3,’Д’>. После этого алгоритм сдвигает влево все содержимое окна на длину совпадающей подстроки и одновременно считывает столько же символов из входного потока в буфер. Получаем в словаре строку «РАММНЫЕ ПРОД», в буфере — «УКТЫ ФИР». В данной ситуации совпадающей подстроки обнаружить не удаться и алгоритм выдаст код <0,0,’У’>, после чего сдвинет окно на один символ. Затем словарь будет содержать «АММНЫЕ ПРОДУ», а буфер — «КТЫ ФИРМ». И т.д.

Декодирование кодов LZ77 проще их получения, т.к. не нужно осуществлять поиск в словаре.

Недостатки LZ77:

• с ростом размеров словаря скорость работы алгоритма-кодера пропорционально замедляется;
• кодирование одиночных символов очень неэффективно.

Кодирование одиночных символов можно сделать эффективным, отказавшись от ненужной ссылки на словарь для них. Кроме того, в некоторые модификации LZ77 для повышения степени сжатия добавляется возможность для кодирования идущих подряд одинаковых символов.

Пример. Закодировать по алгоритму LZ77 строку «КРАСНАЯ КРАСКА».

В последней строчке, буква «А» берется не из словаря, т.к. она последняя.

Длина кода вычисляется следующим образом: длина подстроки не может быть больше размера буфера, а смещение не может быть больше размера словаря . Следовательно, длина двоичного кода смещения будет округленным в большую сторону размер словаря, а длина двоичного кода для длины подстроки будет округленным в большую сторону размер буфера. А символ кодируется 8 битами (например, ASCII+).

В последнем примере длина полученного кода равна бит, против бит исходной длины строки.

В 1982 г. Сторером (Storer) и Шиманским (Szimanski) на базе LZ77 был разработан алгоритм LZSS, который отличается от LZ77 производимыми кодами.

Код, выдаваемый LZSS, начинается с однобитного префикса, различающего собственно код от незакодированного символа. Код состоит из пары: смещение и длина, такими же как и для LZ77. В LZSS окно сдвигается ровно на длину найденной подстроки или на 1, если не найдено вхождение подстроки из буфера в словарь. Длина подстроки в LZSS всегда больше нуля, поэтому длина двоичного кода для длины подстроки — это округленный до большего целого двоичный логарифм от длины буфера.

Пример. Закодировать по алгоритму LZSS строку «КРАСНАЯ КРАСКА».

Здесь длина полученного кода равна бит.

LZ77 и LZSS обладают следующими очевидными недостатками:

1. невозможность кодирования подстрок, отстоящих друг от друга на расстоянии, большем длины словаря;
2. длина подстроки, которую можно закодировать, ограничена размером буфера.

Если механически чрезмерно увеличивать размеры словаря и буфера, то это приведет к снижению эффективности кодирования, т.к. с ростом этих величин будут расти и длины кодов для смещения и длины, что сделает коды для коротких подстрок недопустимо большими. Кроме того, резко увеличится время работы алгоритма-кодера.

В 1978 г. авторами LZ77 был разработан алгоритм LZ78, лишенный названных недостатков.

LZ78 не использует «скользящее» окно, он хранит словарь из уже просмотренных фраз. При старте алгоритма этот словарь содержит только одну пустую строку (строку длины нуль). Алгоритм считывает символы сообщения до тех пор, пока накапливаемая подстрока входит целиком в одну из фраз словаря. Как только эта строка перестанет соответствовать хотя бы одной фразе словаря, алгоритм генерирует код, состоящий из индекса строки в словаре, которая до последнего введенного символа содержала входную строку, и символа, нарушившего совпадение. Затем в словарь добавляется введенная подстрока. Если словарь уже заполнен, то из него предварительно удаляют менее всех используемую в сравнениях фразу.

Ключевым для размера получаемых кодов является размер словаря во фразах, потому что каждый код при кодировании по методу LZ78 содержит номер фразы в словаре. Из последнего следует, что эти коды имеют постоянную длину, равную округленному в большую сторону двоичному логарифму размера словаря (это количество бит в байт-коде расширенного ASCII).

Пример. Закодировать по алгоритму LZ78 строку «КРАСНАЯ КРАСКА», используя словарь длиной 16 фраз.

Указатель на любую фразу такого словаря — это число от 0 до 15, для его кодирования достаточно четырех бит.

В последнем примере длина полученного кода равна битам.

Алгоритмы LZ77, LZ78 и LZSS разработаны математиками и могут использоваться свободно.

В 1984 г. Уэлчем (Welch) был путем модификации LZ78 создан алгоритм LZW.

Пошаговое описание алгоритма-кодера.

Шаг 1. Инициализация словаря всеми возможными односимвольными фразами (обычно 256 символами расширенного ASCII). Инициализация входной фразы w первым символом сообщения.

^ Считать очередной символ K из кодируемого сообщения.

Шаг 3. Если КОНЕЦ_СООБЩЕНИЯ

Выдать код для w

Конец

Если фраза wK уже есть в словаре

Присвоить входной фразе значение wK

Перейти к Шагу 2

Иначе

Выдать код w

Добавить wK в словарь

Присвоить входной фразе значение K

Перейти к Шагу 2.

Как и в случае с LZ78 для LZW ключевым для размера получаемых кодов является размер словаря во фразах: LZW-коды имеют постоянную длину, равную округленному в большую сторону двоичному логарифму размера словаря.

Пример. Закодировать по алгоритму LZW строку «КРАСНАЯ КРАСКА». Размер словаря — 500 фраз.

В этом примере длина полученного кода равна битам.

При переполнении словаря, т.е. когда необходимо внести новую фразу в полностью заполненный словарь, из него удаляют либо наиболее редко используемую фразу, либо все фразы, отличающиеся от одиночного символа.

Алгоритм LZW является запатентованным и, таким образом, представляет собой интеллектуальную собственность. Его безлицензионное использование особенно на аппаратном уровне может повлечь за собой неприятности.

Любопытна история патентования LZW. Заявку на LZW подали почти одновременно две фирмы — сначала IBM и затем Unisys, но первой была рассмотрена заявка Unisys, которая и получила патент. Однако, еще до патентования LZW был использован в широко известной в мире Unix программе сжатия данных compress.

Упражнение 30 Закодировать сообщения «AABCDAACCCCDBB», «КИБЕРНЕТИКИ» и «СИНЯЯ СИНЕВА СИНИ», вычислить длины в битах полученных кодов, используя алгоритмы,

• LZ77 (словарь — 12 байт, буфер — 4 байта),
• LZ78 (словарь — 16 фраз),
• LZSS (словарь — 12 байт, буфер — 4 байта),
• LZW (словарь — ASCII+ и 16 фраз).

Упражнение 31 Может ли для первого символа сообщения код LZ78 быть короче кода LZW при одинаковых размерах словарей? Обосновать. Для LZW в размер словаря не включать позиции для ASCII+.

С того момента, как информация стала переводиться в электронную форму, возникла новая и достаточно сложная проблема. С одной стороны, манипулирование электронными данными стало значительно удобнее и быстрее. Однако, в то же время, достигнутый эффект оказался обманчивым. Выиграв в самом начале, технология породила процесс почти неконтролируемого роста объема электронных файлов. Причем увеличился размер не только операционной системы или пользовательских приложений, создаваемые этими программами рабочие файлы также выросли.
Кроме того, в той или иной электронной форме появились и получили широкое распространение иллюстрации, фотографии, музыкальные композиции, кинофильмы, чертежи, компьютерные игры и многое другое. Достаточно быстро эта информация не только заняла некогда освободившиеся объемы, но и превысила их. Так, согласно практическим наблюдениям, жесткий диск емкостью порядка двух с половиной мегабайт полностью заполняется примерно за шесть-восемь месяцев обычной эксплуатации. Для решения этой проблемы были созданы специализированные программы для упаковки данных. Эти программы получили наименование архиваторов.

Принцип работы архиватора, во всяком случае в теории, достаточно прост. Если детально рассмотреть любой файл чего бы то ни было, то можно обнаружить, что он состоит из некоторого набора нолей и единиц. Их количество и взаимное расположение зависит от того, что это за файл, однако битовая последовательность может быть рассмотрена и с точки зрения комбинаторики. Предположим, есть некоторый фрагмент данных:

110110110110

Независимо от того, кто и для чего его применяет, в фрагменте наблюдается определенная закономерность. Последовательность «110» повторяется четыре раза подряд. Таким образом появляется возможность заменить вышеуказанный фрагмент следующей последовательностью:

КЛЮЧповторповторповтор

Где под ключом обозначается участок 110, а символ повтора означает, что на его месте должен находиться тот ключ, что и в предыдущем. Если условно сказать, что повтор обозначается как 1, то исходный фрагмент преобразуется в:

110111

В результате из последовательности длиной двенадцать бит получается последовательность в шесть бит. То есть применение алгоритма кодирования позволило сжать исходный файл в два раза.

Естественно, в упакованном виде такой файл не может быть использован той программой, которая его создала. Однако это решает проблему хранения данных, в то время, когда надобность в них отпадает. Особенно при резервном копировании, так как за счет сжатия становится возможным гораздо эффективнее использовать имеющееся дисковое пространство персонального компьютера или объем картриджей других систем долговременного хранения электронной информации. Так как программа архивации и разархивации (в последнее время они объединяются в единый модуль) сама по себе занимает достаточно мало места (обычно не более одного мегабайта), то ее размером можно пренебречь.

Собственно говоря, архиваторы уже достаточно давно получили широкое распространение. В частности, даже в операционную систему Microsoft Windows встроен модуль DriveSpice, принцип работы которого основан на динамическом применении алгоритмов сжатия в процессе функционирования самой операционной системы. В случае его установки и активизации Microsoft Windows, при каждом обращении к жесткому диску, он будет упаковывать данные перед операцией записи и распаковывать их при операции чтения. Так как DriveSpice совершенно прозрачен для пользовательских приложений, то его использование как бы увеличивает емкость имеющихся магнитных носителей.

Однако средствами DriveSpice полностью решить проблему эффективного сжатия данных невозможно. Прежде всего потому, что эта утилита значительно уступает специализированным программам данной области по одному из самых важных параметров — плотности упаковки. Иными словами, один и тот же объем одних и тех же неупакованных файлов различными архиваторами сжимается в разной степени. Эта разница может достигать пятидесяти процентов, что более чем значительно.

Различия в плотности упаковки являются прямым следствием разной эффективности использованных математических алгоритмов анализа исходного файла и последующего определения ключей кодирования. Проблема заключается в том, что алгоритм должен не только найти закономерности в потоке бит, но и выделить все возможные варианты исходя из подхода к выбору минимальной длины ключа. Если в приведенном выше примере в качестве ключа взять один бит, то, вместо уплотнения, архиватор, наоборот, создаст архив большего размера. В то же время, ключ объемом в шесть бит также может быть использован для кодирования, ибо эта последовательность дважды повторяется в указанном примере. Таким образом, пример может быть представлен как:

1101101

Однако его длина составляет семь бит, что на единицу больше, чем в первом варианте кодирования. Специализированные программы-архиваторы основываются на более совершенных алгоритмах, поэтому они работают эффективнее.

Вторым, после плотности упаковки, важнейшим показателем эффективности архиватора является время упаковки или распаковки. Действительно, какой прок в высокоэффективной программе сжатия, если результат ее работы появится через несколько лет? Так как первые архиваторы значительно различались между собой и по плотности и по времени упаковки, то в эпоху DOS вокруг их показателей кипели жаркие споры. Однако достаточно быстро стало ясно, что любой, даже самый эффективный алгоритм, чрезвычайно сильно зависит от того, какие данные он будет упаковывать. Текстовые файлы сжимаются значительно сильнее, чем, например, фотография или музыкальная запись. На самом деле текст состоит из весьма ограниченного количества символов. Так, русский текст формируется из тридцати двух букв алфавита и небольшого числа специальных символов, типа запятой, тире и так далее. Пробел между словами также может быть представлен как специальный символ. Следовательно, все многообразие слов любого произведения может быть заменено не более чем шестьюдесятью четырьмя кодовыми знаками. В случае кодирования музыки или графики степень упорядочения данных на несколько порядков меньше, стало быть резко снижается и возможность вычленить среди них подобные участки равной длины. Таким образом один и тот же алгоритм может достичь разных результатов при обработке разных данных.

По мере совершенствования алгоритмов сжатия среди всего многообразия применявшихся программ-архиваторов сформировался своего рода топ-лист лидеров de facto. Среди них оказались архиваторы ZIP, RAR, ARJ и некоторые другие. Так как операционная система Microsoft Windows 95 поддерживала так называемый DOS-режим, то до некоторого времени было возможно использовать в среде Windows программы, созданные только для DOS. Однако их эксплуатация была связана с некоторыми серьезными неудобствами. В частности, DOS-приложения не поддерживали длинные имена файлов, а также имена, содержащие символы кириллицы. Кроме того, постоянная необходимость «выходить в DOS» для обращения к архиву также не могла доставить удовольствие пользователям Windows.

Все это вместе взятое инициализировало создание архиваторов и для новой операционной системы фирмы Microsoft. Естественно, что в самую первую очередь для Microsoft Windows были переработаны лидирующие архиваторы ввиду их широкого распространения среди пользователей. Далее мы рассмотрим две из них, пользующиеся наибольшей популярностью: WinZIP и WinRAR 95.

Достаточно бессмысленно определять, какая из них является самой лучшей. Во-первых, различия в эффективности их применения сколько-нибудь заметно проявляются лишь при архивации очень больших объемов, порядка нескольких сотен мегабайт, однородных файлов. В реальных условиях подобное происходит крайне редко. Гораздо чаще архивации подвергаются разнородные данные, что в значительной мере нивелирует преимущества и недостатки использованных математических и программных алгоритмов. Может возникнуть мысль, что целесообразно иметь несколько архиваторов для разных типов данных. Однако практически такое еще менее удобно, так как перед обращением к данным приходится еще определять, каким инструментом это делать, и проводить предварительную сортировку файлов.

Если просуммировать все эти обстоятельства, то при выборе архиватора прежде всего следует руководствоваться следующими критериями:

a) Какой тип архивов уже существует в рамках той рабочей группы, в которой вам предстоит взаимодействовать. Если речь идет о выборе архиватора для личного использования, то этот критерий отпадает.

b) Какие объемы предполагается сжимать. Если единовременный набор файлов велик или если впоследствии архивы будут переноситься между компьютерами любым другим способом, кроме локальной вычислительной сети, то целесообразно выяснить, поддерживает ли конкретный архиватор такую опцию, как создание большого архива в виде нескольких томов малого объема. Обычно, если такая опция поддерживается, то в интерфейс программы уже заранее встроена возможность создания томов размера, кратного наиболее популярным носителям данных, например трехдюймовой дискете емкостью 1,44 Мб.

c) Какой тип данных среди архивируемой информации преобладает. Если более трех четвертей состоит из однородных данных, то желательно выбирать архиватор, чьи преимущества в этом случае проявляются более всего. Определенное отставание в остальных случаях на общем фоне окажется практически незаметным.

И последним элементом, по которому нелишне оценить архиватор перед выбором, это удобство его интерфейса. В конце концов, именно вам придется постоянно общаться с этой программой. Если это окажется слишком обременительным или чрезвычайно многоходовым, то скорее всего вы достаточно скоро откажетесь от него и будете вынуждены потратить достаточно много времени на перекодирование всех ранее созданных архивов.
Продолжение следует

Александр Запольскис