Vehicle routing problem with time windows - Доктор Windows - ваш надежный помощник

Stay organized with collections

Save and categorize content based on your preferences.

Many vehicle routing problems involve scheduling visits to customers who are
only available during specific time windows.

These problems are known as vehicle routing problems with time windows (VRPTWs).

VRPTW Example

On this page, we’ll walk through an example that shows how to solve a VRPTW.
Since the problem involves time windows, the data include a time matrix,
which contains the travel times between locations (rather than a distance matrix
as in previous examples).

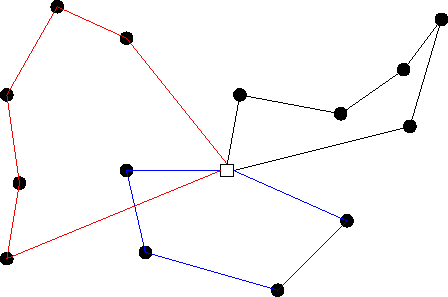
The diagram below shows the locations to visit in blue and the depot in black.
The time windows are shown above each location. See
Location coordinates in the
VRP section for more details about how the locations are defined.

The goal is to minimize the total travel time of the vehicles.

The following sections describe how to solve the VRPTW example with OR-Tools.

Create the data

The following function creates the data for the problem.

Python

def create_data_model():
    """Stores the data for the problem."""
    data = {}
    data['time_matrix'] = [
        [0, 6, 9, 8, 7, 3, 6, 2, 3, 2, 6, 6, 4, 4, 5, 9, 7],
        [6, 0, 8, 3, 2, 6, 8, 4, 8, 8, 13, 7, 5, 8, 12, 10, 14],
        [9, 8, 0, 11, 10, 6, 3, 9, 5, 8, 4, 15, 14, 13, 9, 18, 9],
        [8, 3, 11, 0, 1, 7, 10, 6, 10, 10, 14, 6, 7, 9, 14, 6, 16],
        [7, 2, 10, 1, 0, 6, 9, 4, 8, 9, 13, 4, 6, 8, 12, 8, 14],
        [3, 6, 6, 7, 6, 0, 2, 3, 2, 2, 7, 9, 7, 7, 6, 12, 8],
        [6, 8, 3, 10, 9, 2, 0, 6, 2, 5, 4, 12, 10, 10, 6, 15, 5],
        [2, 4, 9, 6, 4, 3, 6, 0, 4, 4, 8, 5, 4, 3, 7, 8, 10],
        [3, 8, 5, 10, 8, 2, 2, 4, 0, 3, 4, 9, 8, 7, 3, 13, 6],
        [2, 8, 8, 10, 9, 2, 5, 4, 3, 0, 4, 6, 5, 4, 3, 9, 5],
        [6, 13, 4, 14, 13, 7, 4, 8, 4, 4, 0, 10, 9, 8, 4, 13, 4],
        [6, 7, 15, 6, 4, 9, 12, 5, 9, 6, 10, 0, 1, 3, 7, 3, 10],
        [4, 5, 14, 7, 6, 7, 10, 4, 8, 5, 9, 1, 0, 2, 6, 4, 8],
        [4, 8, 13, 9, 8, 7, 10, 3, 7, 4, 8, 3, 2, 0, 4, 5, 6],
        [5, 12, 9, 14, 12, 6, 6, 7, 3, 3, 4, 7, 6, 4, 0, 9, 2],
        [9, 10, 18, 6, 8, 12, 15, 8, 13, 9, 13, 3, 4, 5, 9, 0, 9],
        [7, 14, 9, 16, 14, 8, 5, 10, 6, 5, 4, 10, 8, 6, 2, 9, 0],
    ]
    data['time_windows'] = [
        (0, 5),  # depot
        (7, 12),  # 1
        (10, 15),  # 2
        (16, 18),  # 3
        (10, 13),  # 4
        (0, 5),  # 5
        (5, 10),  # 6
        (0, 4),  # 7
        (5, 10),  # 8
        (0, 3),  # 9
        (10, 16),  # 10
        (10, 15),  # 11
        (0, 5),  # 12
        (5, 10),  # 13
        (7, 8),  # 14
        (10, 15),  # 15
        (11, 15),  # 16
    ]
    data['num_vehicles'] = 4
    data['depot'] = 0
    return data

The data consists of:

data['time_matrix']: An array of travel times between locations.
Note that this differs from previous examples, which use a distance matrix. If
all vehicles travel at the same speed, you will get the same solution if you
use a distance matrix or a time matrix, since travel distances are a constant
multiple of travel times.
data['time_windows']: An array of time windows for the locations,
which you can think of as requested times for a visit. Vehicles must visit a
location within its time window.
data['num_vehicles']: The number of vehicles in the fleet.
data['depot']: The index of the depot.

C++

struct DataModel {
  const std::vector<std::vector<int64_t>> time_matrix{
      {0, 6, 9, 8, 7, 3, 6, 2, 3, 2, 6, 6, 4, 4, 5, 9, 7},
      {6, 0, 8, 3, 2, 6, 8, 4, 8, 8, 13, 7, 5, 8, 12, 10, 14},
      {9, 8, 0, 11, 10, 6, 3, 9, 5, 8, 4, 15, 14, 13, 9, 18, 9},
      {8, 3, 11, 0, 1, 7, 10, 6, 10, 10, 14, 6, 7, 9, 14, 6, 16},
      {7, 2, 10, 1, 0, 6, 9, 4, 8, 9, 13, 4, 6, 8, 12, 8, 14},
      {3, 6, 6, 7, 6, 0, 2, 3, 2, 2, 7, 9, 7, 7, 6, 12, 8},
      {6, 8, 3, 10, 9, 2, 0, 6, 2, 5, 4, 12, 10, 10, 6, 15, 5},
      {2, 4, 9, 6, 4, 3, 6, 0, 4, 4, 8, 5, 4, 3, 7, 8, 10},
      {3, 8, 5, 10, 8, 2, 2, 4, 0, 3, 4, 9, 8, 7, 3, 13, 6},
      {2, 8, 8, 10, 9, 2, 5, 4, 3, 0, 4, 6, 5, 4, 3, 9, 5},
      {6, 13, 4, 14, 13, 7, 4, 8, 4, 4, 0, 10, 9, 8, 4, 13, 4},
      {6, 7, 15, 6, 4, 9, 12, 5, 9, 6, 10, 0, 1, 3, 7, 3, 10},
      {4, 5, 14, 7, 6, 7, 10, 4, 8, 5, 9, 1, 0, 2, 6, 4, 8},
      {4, 8, 13, 9, 8, 7, 10, 3, 7, 4, 8, 3, 2, 0, 4, 5, 6},
      {5, 12, 9, 14, 12, 6, 6, 7, 3, 3, 4, 7, 6, 4, 0, 9, 2},
      {9, 10, 18, 6, 8, 12, 15, 8, 13, 9, 13, 3, 4, 5, 9, 0, 9},
      {7, 14, 9, 16, 14, 8, 5, 10, 6, 5, 4, 10, 8, 6, 2, 9, 0},
  };
  const std::vector<std::pair<int64_t, int64_t>> time_windows{
      {0, 5},    // depot
      {7, 12},   // 1
      {10, 15},  // 2
      {16, 18},  // 3
      {10, 13},  // 4
      {0, 5},    // 5
      {5, 10},   // 6
      {0, 4},    // 7
      {5, 10},   // 8
      {0, 3},    // 9
      {10, 16},  // 10
      {10, 15},  // 11
      {0, 5},    // 12
      {5, 10},   // 13
      {7, 8},    // 14
      {10, 15},  // 15
      {11, 15},  // 16
  };
  const int num_vehicles = 4;
  const RoutingIndexManager::NodeIndex depot{0};
};

The data consists of:

time_matrix: An array of travel times between locations.
Note that this differs from previous examples, which use a distance matrix. If
all vehicles travel at the same speed, you will get the same solution if you
use a distance matrix or a time matrix, since travel distances are a constant
multiple of travel times.
time_windows: An array of time windows for the locations,
which you can think of as requested times for a visit. Vehicles must visit a
location within its time window.
num_vehicles: The number of vehicles in the fleet.
depot: The index of the depot.

Java

static class DataModel {
  public final long[][] timeMatrix = {
      {0, 6, 9, 8, 7, 3, 6, 2, 3, 2, 6, 6, 4, 4, 5, 9, 7},
      {6, 0, 8, 3, 2, 6, 8, 4, 8, 8, 13, 7, 5, 8, 12, 10, 14},
      {9, 8, 0, 11, 10, 6, 3, 9, 5, 8, 4, 15, 14, 13, 9, 18, 9},
      {8, 3, 11, 0, 1, 7, 10, 6, 10, 10, 14, 6, 7, 9, 14, 6, 16},
      {7, 2, 10, 1, 0, 6, 9, 4, 8, 9, 13, 4, 6, 8, 12, 8, 14},
      {3, 6, 6, 7, 6, 0, 2, 3, 2, 2, 7, 9, 7, 7, 6, 12, 8},
      {6, 8, 3, 10, 9, 2, 0, 6, 2, 5, 4, 12, 10, 10, 6, 15, 5},
      {2, 4, 9, 6, 4, 3, 6, 0, 4, 4, 8, 5, 4, 3, 7, 8, 10},
      {3, 8, 5, 10, 8, 2, 2, 4, 0, 3, 4, 9, 8, 7, 3, 13, 6},
      {2, 8, 8, 10, 9, 2, 5, 4, 3, 0, 4, 6, 5, 4, 3, 9, 5},
      {6, 13, 4, 14, 13, 7, 4, 8, 4, 4, 0, 10, 9, 8, 4, 13, 4},
      {6, 7, 15, 6, 4, 9, 12, 5, 9, 6, 10, 0, 1, 3, 7, 3, 10},
      {4, 5, 14, 7, 6, 7, 10, 4, 8, 5, 9, 1, 0, 2, 6, 4, 8},
      {4, 8, 13, 9, 8, 7, 10, 3, 7, 4, 8, 3, 2, 0, 4, 5, 6},
      {5, 12, 9, 14, 12, 6, 6, 7, 3, 3, 4, 7, 6, 4, 0, 9, 2},
      {9, 10, 18, 6, 8, 12, 15, 8, 13, 9, 13, 3, 4, 5, 9, 0, 9},
      {7, 14, 9, 16, 14, 8, 5, 10, 6, 5, 4, 10, 8, 6, 2, 9, 0},
  };
  public final long[][] timeWindows = {
    {0, 5}, // depot
    {7, 12}, // 1
    {10, 15}, // 2
    {16, 18}, // 3
    {10, 13}, // 4
    {0, 5}, // 5
    {5, 10}, // 6
    {0, 4}, // 7
    {5, 10}, // 8
    {0, 3}, // 9
    {10, 16}, // 10
    {10, 15}, // 11
    {0, 5}, // 12
    {5, 10}, // 13
    {7, 8}, // 14
    {10, 15}, // 15
    {11, 15}, // 16
  };
  public final int  vehicleNumber = 4;
  public final int  depot = 0;
}

The data consists of:

timeMatrix: An array of travel times between locations.
Note that this differs from previous examples, which use a distance matrix. If
all vehicles travel at the same speed, you will get the same solution if you
use a distance matrix or a time matrix, since travel distances are a constant
multiple of travel times.
timeWindows: An array of time windows for the locations,
which you can think of as requested times for a visit. Vehicles must visit a
location within its time window.
vehicleNumber: The number of vehicles in the fleet.
depot: The index of the depot.

C#

class DataModel
{
    public long[,] TimeMatrix = {
        { 0, 6, 9, 8, 7, 3, 6, 2, 3, 2, 6, 6, 4, 4, 5, 9, 7 },
        { 6, 0, 8, 3, 2, 6, 8, 4, 8, 8, 13, 7, 5, 8, 12, 10, 14 },
        { 9, 8, 0, 11, 10, 6, 3, 9, 5, 8, 4, 15, 14, 13, 9, 18, 9 },
        { 8, 3, 11, 0, 1, 7, 10, 6, 10, 10, 14, 6, 7, 9, 14, 6, 16 },
        { 7, 2, 10, 1, 0, 6, 9, 4, 8, 9, 13, 4, 6, 8, 12, 8, 14 },
        { 3, 6, 6, 7, 6, 0, 2, 3, 2, 2, 7, 9, 7, 7, 6, 12, 8 },
        { 6, 8, 3, 10, 9, 2, 0, 6, 2, 5, 4, 12, 10, 10, 6, 15, 5 },
        { 2, 4, 9, 6, 4, 3, 6, 0, 4, 4, 8, 5, 4, 3, 7, 8, 10 },
        { 3, 8, 5, 10, 8, 2, 2, 4, 0, 3, 4, 9, 8, 7, 3, 13, 6 },
        { 2, 8, 8, 10, 9, 2, 5, 4, 3, 0, 4, 6, 5, 4, 3, 9, 5 },
        { 6, 13, 4, 14, 13, 7, 4, 8, 4, 4, 0, 10, 9, 8, 4, 13, 4 },
        { 6, 7, 15, 6, 4, 9, 12, 5, 9, 6, 10, 0, 1, 3, 7, 3, 10 },
        { 4, 5, 14, 7, 6, 7, 10, 4, 8, 5, 9, 1, 0, 2, 6, 4, 8 },
        { 4, 8, 13, 9, 8, 7, 10, 3, 7, 4, 8, 3, 2, 0, 4, 5, 6 },
        { 5, 12, 9, 14, 12, 6, 6, 7, 3, 3, 4, 7, 6, 4, 0, 9, 2 },
        { 9, 10, 18, 6, 8, 12, 15, 8, 13, 9, 13, 3, 4, 5, 9, 0, 9 },
        { 7, 14, 9, 16, 14, 8, 5, 10, 6, 5, 4, 10, 8, 6, 2, 9, 0 },
    };
    public long[,] TimeWindows = {
        { 0, 5 },   // depot
        { 7, 12 },  // 1
        { 10, 15 }, // 2
        { 16, 18 }, // 3
        { 10, 13 }, // 4
        { 0, 5 },   // 5
        { 5, 10 },  // 6
        { 0, 4 },   // 7
        { 5, 10 },  // 8
        { 0, 3 },   // 9
        { 10, 16 }, // 10
        { 10, 15 }, // 11
        { 0, 5 },   // 12
        { 5, 10 },  // 13
        { 7, 8 },   // 14
        { 10, 15 }, // 15
        { 11, 15 }, // 16
    };
    public int VehicleNumber = 4;
    public int Depot = 0;
};

The data consists of:

TimeMatrix: An array of travel times between locations.
Note that this differs from previous examples, which use a distance matrix. If
all vehicles travel at the same speed, you will get the same solution if you
use a distance matrix or a time matrix, since travel distances are a constant
multiple of travel times.
TimeWindows: An array of time windows for the locations,
which you can think of as requested times for a visit. Vehicles must visit a
location within its time window.
VehicleNumber: The number of vehicles in the fleet.
Depot: The index of the depot.

Time callback

The following function creates the time callback and passes it to the solver. It
also sets the arc costs, which define the cost of travel, to be the travel times
between locations.

Python

def time_callback(from_index, to_index):
    """Returns the travel time between the two nodes."""
    # Convert from routing variable Index to time matrix NodeIndex.
    from_node = manager.IndexToNode(from_index)
    to_node = manager.IndexToNode(to_index)
    return data['time_matrix'][from_node][to_node]

transit_callback_index = routing.RegisterTransitCallback(time_callback)
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)

C++

const int transit_callback_index = routing.RegisterTransitCallback(
    [&data, &manager](int64_t from_index, int64_t to_index) -> int64_t {
      // Convert from routing variable Index to time matrix NodeIndex.
      auto from_node = manager.IndexToNode(from_index).value();
      auto to_node = manager.IndexToNode(to_index).value();
      return data.time_matrix[from_node][to_node];
    });
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);

Java

final int transitCallbackIndex =
    routing.registerTransitCallback((long fromIndex, long toIndex) -> {
      // Convert from routing variable Index to user NodeIndex.
      int fromNode = manager.indexToNode(fromIndex);
      int toNode = manager.indexToNode(toIndex);
      return data.timeMatrix[fromNode][toNode];
    });
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);

C#

int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
                                                           {
                                                               // Convert from routing variable Index to time
                                                               // matrix NodeIndex.
                                                               var fromNode = manager.IndexToNode(fromIndex);
                                                               var toNode = manager.IndexToNode(toIndex);
                                                               return data.TimeMatrix[fromNode, toNode];
                                                           });
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);

Add time window constraints

The following code adds time window constraints for all locations.

Python

time = 'Time'
routing.AddDimension(
    transit_callback_index,
    30,  # allow waiting time
    30,  # maximum time per vehicle
    False,  # Don't force start cumul to zero.
    time)
time_dimension = routing.GetDimensionOrDie(time)
# Add time window constraints for each location except depot.
for location_idx, time_window in enumerate(data['time_windows']):
    if location_idx == data['depot']:
        continue
    index = manager.NodeToIndex(location_idx)
    time_dimension.CumulVar(index).SetRange(time_window[0], time_window[1])
# Add time window constraints for each vehicle start node.
depot_idx = data['depot']
for vehicle_id in range(data['num_vehicles']):
    index = routing.Start(vehicle_id)
    time_dimension.CumulVar(index).SetRange(
        data['time_windows'][depot_idx][0],
        data['time_windows'][depot_idx][1])
for i in range(data['num_vehicles']):
    routing.AddVariableMinimizedByFinalizer(
        time_dimension.CumulVar(routing.Start(i)))
    routing.AddVariableMinimizedByFinalizer(
        time_dimension.CumulVar(routing.End(i)))

C++

std::string time{"Time"};
routing.AddDimension(transit_callback_index,  // transit callback index
                     int64_t{30},             // allow waiting time
                     int64_t{30},             // maximum time per vehicle
                     false,  // Don't force start cumul to zero
                     time);
const RoutingDimension& time_dimension = routing.GetDimensionOrDie(time);
// Add time window constraints for each location except depot.
for (int i = 1; i < data.time_windows.size(); ++i) {
  int64_t index = manager.NodeToIndex(RoutingIndexManager::NodeIndex(i));
  time_dimension.CumulVar(index)->SetRange(data.time_windows[i].first,
                                           data.time_windows[i].second);
}
// Add time window constraints for each vehicle start node.
for (int i = 0; i < data.num_vehicles; ++i) {
  int64_t index = routing.Start(i);
  time_dimension.CumulVar(index)->SetRange(data.time_windows[0].first,
                                           data.time_windows[0].second);
}
for (int i = 0; i < data.num_vehicles; ++i) {
  routing.AddVariableMinimizedByFinalizer(
      time_dimension.CumulVar(routing.Start(i)));
  routing.AddVariableMinimizedByFinalizer(
      time_dimension.CumulVar(routing.End(i)));
}

Java

routing.addDimension(transitCallbackIndex, // transit callback
    30, // allow waiting time
    30, // vehicle maximum capacities
    false, // start cumul to zero
    "Time");
RoutingDimension timeDimension = routing.getMutableDimension("Time");
// Add time window constraints for each location except depot.
for (int i = 1; i < data.timeWindows.length; ++i) {
  long index = manager.nodeToIndex(i);
  timeDimension.cumulVar(index).setRange(data.timeWindows[i][0], data.timeWindows[i][1]);
}
// Add time window constraints for each vehicle start node.
for (int i = 0; i < data.vehicleNumber; ++i) {
  long index = routing.start(i);
  timeDimension.cumulVar(index).setRange(data.timeWindows[0][0], data.timeWindows[0][1]);
}
for (int i = 0; i < data.vehicleNumber; ++i) {
  routing.addVariableMinimizedByFinalizer(timeDimension.cumulVar(routing.start(i)));
  routing.addVariableMinimizedByFinalizer(timeDimension.cumulVar(routing.end(i)));
}

C#

routing.AddDimension(transitCallbackIndex, // transit callback
                     30,                   // allow waiting time
                     30,                   // vehicle maximum capacities
                     false,                // start cumul to zero
                     "Time");
RoutingDimension timeDimension = routing.GetMutableDimension("Time");
// Add time window constraints for each location except depot.
for (int i = 1; i < data.TimeWindows.GetLength(0); ++i)
{
    long index = manager.NodeToIndex(i);
    timeDimension.CumulVar(index).SetRange(data.TimeWindows[i, 0], data.TimeWindows[i, 1]);
}
// Add time window constraints for each vehicle start node.
for (int i = 0; i < data.VehicleNumber; ++i)
{
    long index = routing.Start(i);
    timeDimension.CumulVar(index).SetRange(data.TimeWindows[0, 0], data.TimeWindows[0, 1]);
}
for (int i = 0; i < data.VehicleNumber; ++i)
{
    routing.AddVariableMinimizedByFinalizer(timeDimension.CumulVar(routing.Start(i)));
    routing.AddVariableMinimizedByFinalizer(timeDimension.CumulVar(routing.End(i)));
}

The code creates a dimension for the travel
time of the vehicles, similar to the dimensions for travel distance or demands
in previous examples. Dimensions keep track of quantities that accumulate over a
vehicle’s route. In the code above, time_dimension.CumulVar(index) is
the cumulative travel time when a vehicle arrives at the
location with the given index.

The dimension is created using the AddDimension method, which has the
following arguments:

The index for the travel time callback: transit_callback_index
An upper bound for slack (the wait times at the locations): 30. While this
was set to 0 in the CVRP example, the
VRPTW has to allow positive wait time due to the time window constraints.
An upper bound for the total time over each vehicle’s route: 30
A boolean variable that specifies whether the cumulative variable is set to
zero at the start of each vehicle’s route.
The name of the dimension.

Next, the lines

timeDimension.CumulVar(index).SetRange(
    data.TimeWindows[0, 0],
    data.TimeWindows[0, 1]);

require that a vehicle must visit a location during the location’s time window.

Set search parameters

The following code sets the default search parameters and a heuristic method for
finding the first solution:

Python

search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.first_solution_strategy = (
    routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC)

C++

RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
searchParameters.set_first_solution_strategy(
    FirstSolutionStrategy::PATH_CHEAPEST_ARC);

Java

RoutingSearchParameters searchParameters =
    main.defaultRoutingSearchParameters()
        .toBuilder()
        .setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
        .build();

C#

RoutingSearchParameters searchParameters =
    operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;

Add the solution printer

The function that displays the solution is shown below.

Python

def print_solution(data, manager, routing, solution):
    """Prints solution on console."""
    print(f'Objective: {solution.ObjectiveValue()}')
    time_dimension = routing.GetDimensionOrDie('Time')
    total_time = 0
    for vehicle_id in range(data['num_vehicles']):
        index = routing.Start(vehicle_id)
        plan_output = 'Route for vehicle {}:n'.format(vehicle_id)
        while not routing.IsEnd(index):
            time_var = time_dimension.CumulVar(index)
            plan_output += '{0} Time({1},{2}) -> '.format(
                manager.IndexToNode(index), solution.Min(time_var),
                solution.Max(time_var))
            index = solution.Value(routing.NextVar(index))
        time_var = time_dimension.CumulVar(index)
        plan_output += '{0} Time({1},{2})n'.format(manager.IndexToNode(index),
                                                    solution.Min(time_var),
                                                    solution.Max(time_var))
        plan_output += 'Time of the route: {}minn'.format(
            solution.Min(time_var))
        print(plan_output)
        total_time += solution.Min(time_var)
    print('Total time of all routes: {}min'.format(total_time))

C++

//! @brief Print the solution.
//! @param[in] data Data of the problem.
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const DataModel& data, const RoutingIndexManager& manager,
                   const RoutingModel& routing, const Assignment& solution) {
  const RoutingDimension& time_dimension = routing.GetDimensionOrDie("Time");
  int64_t total_time{0};
  for (int vehicle_id = 0; vehicle_id < data.num_vehicles; ++vehicle_id) {
    int64_t index = routing.Start(vehicle_id);
    LOG(INFO) << "Route for vehicle " << vehicle_id << ":";
    std::ostringstream route;
    while (routing.IsEnd(index) == false) {
      auto time_var = time_dimension.CumulVar(index);
      route << manager.IndexToNode(index).value() << " Time("
            << solution.Min(time_var) << ", " << solution.Max(time_var)
            << ") -> ";
      index = solution.Value(routing.NextVar(index));
    }
    auto time_var = time_dimension.CumulVar(index);
    LOG(INFO) << route.str() << manager.IndexToNode(index).value() << " Time("
              << solution.Min(time_var) << ", " << solution.Max(time_var)
              << ")";
    LOG(INFO) << "Time of the route: " << solution.Min(time_var) << "min";
    total_time += solution.Min(time_var);
  }
  LOG(INFO) << "Total time of all routes: " << total_time << "min";
  LOG(INFO) << "";
  LOG(INFO) << "Advanced usage:";
  LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}

Java

/// @brief Print the solution.
static void printSolution(
    DataModel data, RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
  // Solution cost.
  logger.info("Objective : " + solution.objectiveValue());
  // Inspect solution.
  RoutingDimension timeDimension = routing.getMutableDimension("Time");
  long totalTime = 0;
  for (int i = 0; i < data.vehicleNumber; ++i) {
    long index = routing.start(i);
    logger.info("Route for Vehicle " + i + ":");
    String route = "";
    while (!routing.isEnd(index)) {
      IntVar timeVar = timeDimension.cumulVar(index);
      route += manager.indexToNode(index) + " Time(" + solution.min(timeVar) + ","
          + solution.max(timeVar) + ") -> ";
      index = solution.value(routing.nextVar(index));
    }
    IntVar timeVar = timeDimension.cumulVar(index);
    route += manager.indexToNode(index) + " Time(" + solution.min(timeVar) + ","
        + solution.max(timeVar) + ")";
    logger.info(route);
    logger.info("Time of the route: " + solution.min(timeVar) + "min");
    totalTime += solution.min(timeVar);
  }
  logger.info("Total time of all routes: " + totalTime + "min");
}

C#

/// <summary>
///   Print the solution.
/// </summary>
static void PrintSolution(in DataModel data, in RoutingModel routing, in RoutingIndexManager manager,
                          in Assignment solution)
{
    Console.WriteLine($"Objective {solution.ObjectiveValue()}:");

    // Inspect solution.
    RoutingDimension timeDimension = routing.GetMutableDimension("Time");
    long totalTime = 0;
    for (int i = 0; i < data.VehicleNumber; ++i)
    {
        Console.WriteLine("Route for Vehicle {0}:", i);
        var index = routing.Start(i);
        while (routing.IsEnd(index) == false)
        {
            var timeVar = timeDimension.CumulVar(index);
            Console.Write("{0} Time({1},{2}) -> ", manager.IndexToNode(index), solution.Min(timeVar),
                          solution.Max(timeVar));
            index = solution.Value(routing.NextVar(index));
        }
        var endTimeVar = timeDimension.CumulVar(index);
        Console.WriteLine("{0} Time({1},{2})", manager.IndexToNode(index), solution.Min(endTimeVar),
                          solution.Max(endTimeVar));
        Console.WriteLine("Time of the route: {0}min", solution.Min(endTimeVar));
        totalTime += solution.Min(endTimeVar);
    }
    Console.WriteLine("Total time of all routes: {0}min", totalTime);
}

The solution displays the vehicle routes, and the solution window at each
location, as explained in the next section.

Solution windows

The solution window at a location is the time interval during which a
vehicle must arrive, in order to stay on schedule.The solution window is
contained in—and usually smaller than—the
constraint time window at the location.

In the solution printer function above, the solution window is returned by
(assignment.Min(time_var), assignment.Max(time_var) where
time_var = time_dimension.CumulVar(index) is the vehicle’s cumulative travel
time at the location.

If the minimum and maximum values of time_var are the same, the solution
window is a single point in time, which means the vehicle must depart from the
location as soon as it arrives. On the other hand, if the minimum is less than
the maximum, the vehicle can wait before departing.

The section Running the program describes the solution windows for
this example.

Solve

The main function for this example is similar to the one for the
TSP example.

Python

solution = routing.SolveWithParameters(search_parameters)

C++

const Assignment* solution = routing.SolveWithParameters(searchParameters);

Java

Assignment solution = routing.solveWithParameters(searchParameters);

C#

Assignment solution = routing.SolveWithParameters(searchParameters);

Running the program

When you run the program, it displays the
following output:

Route for vehicle 0:
 0 Time(0,0) ->  9 Time(2,3) ->  14 Time(7,8) -> 16 Time(11,11) ->  0 Time(18,18)
Time of the route: 18min

Route for vehicle 1:
 0 Time(0,0) -> 7 Time(2,4) -> 1 Time(7,11) -> 4 Time(10,13) -> 3 Time(16,16) -> 0 Time(24,24)
Time of the route: 24min

Route for vehicle 2:
 0 Time(0,0) -> 12 Time(4,4) -> 13 Time(6,6) -> 15 Time(11,11) -> 11 Time(14,14) -> 0 Time(20,20)
Time of the route: 20min

Route for vehicle 3:
 0 Time(0,0) -> 5 Time(3,3) -> 8 Time(5,5) -> 6 Time(7,7) -> 2 Time(10,10) -> 10 Time(14,14) ->
 0 Time(20,20)
Time of the route: 20min

Total time of all routes: 82min

For each location on a route, Time(a,b) is the
solution window: the vehicle that visits the location must
do so in that time interval to stay on schedule.

As an example, take a look at the following portion of the route for vehicle 0.

0 Time(0,0) -> 9 Time(2,3) -> 14 Time(7,8)

At location 9, the solution window is Time(2,3), which means the vehicle must
arrive there between times 2 and 3. Note that the solution window is contained
in the constraint time window at that location, (0, 3), given in the
problem data. The solution window starts at time 2 because it takes 2 units of
time (the 0, 9 entry of the time matrix) to get from the depot to
location 9.

Why can the vehicle depart location 9 anytime between 2 and 3? The reason is
that since the travel time from location 9 to location 14 is 3, if the vehicle
leaves anytime before 3, it will arrive at location 14 before time 6, which is
too early for its visit. So the vehicle has to wait somewhere, e.g., the driver
could decide to wait at location 9 until time 3 without delaying completion of
the route.

You may have noticed that some solution windows (e.g. at locations 9 and 14)
have different start and end times, but others (e.g. on routes 2 and 3) have the
same start and end time. In the former case, the vehicles can wait until the end
of the window before departing, while in the latter, they must depart as soon as
they arrive.

Save the solution windows to a list or array

The TSP section shows how to save the routes
in a solution to a list or array. For a VRPTW, you can also save the
solution windows.
The functions below save the solution windows to a list (Python) or an array (C++).

Python

def get_cumul_data(solution, routing, dimension):
  """Get cumulative data from a dimension and store it in an array."""
  # Returns an array cumul_data whose i,j entry contains the minimum and
  # maximum of CumulVar for the dimension at the jth node on route :
  # - cumul_data[i][j][0] is the minimum.
  # - cumul_data[i][j][1] is the maximum.

  cumul_data = []
  for route_nbr in range(routing.vehicles()):
    route_data = []
    index = routing.Start(route_nbr)
    dim_var = dimension.CumulVar(index)
    route_data.append([solution.Min(dim_var), solution.Max(dim_var)])
    while not routing.IsEnd(index):
      index = solution.Value(routing.NextVar(index))
      dim_var = dimension.CumulVar(index)
      route_data.append([solution.Min(dim_var), solution.Max(dim_var)])
    cumul_data.append(route_data)
  return cumul_data

C++

std::vector<std::vector<std::pair<int64_t, int64_t>>> GetCumulData(
    const Assignment& solution, const RoutingModel& routing,
    const RoutingDimension& dimension) {
  // Returns an array cumul_data, whose i, j entry is a pair containing
  // the minimum and maximum of CumulVar for the dimension.:
  // - cumul_data[i][j].first is the minimum.
  // - cumul_data[i][j].second is the maximum.
  std::vector<std::vector<std::pair<int64_t, int64_t>>> cumul_data(
      routing.vehicles());

  for (int vehicle_id = 0; vehicle_id < routing.vehicles(); ++vehicle_id) {
    int64_t index = routing.Start(vehicle_id);
    IntVar* dim_var = dimension.CumulVar(index);
    cumul_data[vehicle_id].emplace_back(solution.Min(dim_var),
                                        solution.Max(dim_var));
    while (!routing.IsEnd(index)) {
      index = solution.Value(routing.NextVar(index));
      IntVar* dim_var = dimension.CumulVar(index);
      cumul_data[vehicle_id].emplace_back(solution.Min(dim_var),
                                          solution.Max(dim_var));
    }
  }
  return cumul_data;
}

The functions save the minimum and maximum values of the cumulative data for any
dimension (not just time).
In the current example, these values are the lower and upper bounds of the
solution window, and the dimension passed to the function is
time_dimension.

The following functions print the solution from the
routes and the cumulative data.

Python

def print_solution(routes, cumul_data):
  """Print the solution."""
  total_time = 0
  route_str = ''
  for i, route in enumerate(routes):
    route_str += 'Route ' + str(i) + ':n'
    start_time = cumul_data[i][0][0]
    end_time = cumul_data[i][0][1]
    route_str += '  ' + str(route[0]) + 
                 ' Time(' + str(start_time) + ', ' + str(end_time) + ')'
    for j in range(1, len(route)):
      start_time = cumul_data[i][j][0]
      end_time = cumul_data[i][j][1]
      route_str += ' -> ' + str(route[j]) + 
                   ' Time(' + str(start_time) + ', ' + str(end_time) + ')'
    route_str += 'n  Route time: {} minnn'.format(start_time)
    total_time += cumul_data[i][len(route) - 1][0]
  route_str += 'Total time: {} min'.format(total_time)
  print(route_str)

C++

void PrintSolution(
    const std::vector<std::vector<int>> routes,
    std::vector<std::vector<std::pair<int64_t, int64_t>>> cumul_data) {
  int64_t total_time{0};
  std::ostringstream route;
  for (int vehicle_id = 0; vehicle_id < routes.size(); ++vehicle_id) {
    route << "nRoute " << vehicle_id << ": n";

    route << "  " << routes[vehicle_id][0] << " Time("
          << cumul_data[vehicle_id][0].first << ", "
          << cumul_data[vehicle_id][0].second << ") ";
    for (int j = 1; j < routes[vehicle_id].size(); ++j) {
      route << "-> " << routes[vehicle_id][j] << " Time("
            << cumul_data[vehicle_id][j].first << ", "
            << cumul_data[vehicle_id][j].second << ") ";
    }
    route << "n  Route time: "
          << cumul_data[vehicle_id][routes[vehicle_id].size() - 1].first
          << " minutesn";

    total_time += cumul_data[vehicle_id][routes[vehicle_id].size() - 1].first;
  }
  route << "nTotal travel time: " << total_time << " minutes";
  LOG(INFO) << route.str();
}

Complete programs

The complete programs for the vehicle routing problem with time windows are
shown below.

Python

"""Vehicles Routing Problem (VRP) with Time Windows."""

from ortools.constraint_solver import routing_enums_pb2
from ortools.constraint_solver import pywrapcp


def create_data_model():
    """Stores the data for the problem."""
    data = {}
    data['time_matrix'] = [
        [0, 6, 9, 8, 7, 3, 6, 2, 3, 2, 6, 6, 4, 4, 5, 9, 7],
        [6, 0, 8, 3, 2, 6, 8, 4, 8, 8, 13, 7, 5, 8, 12, 10, 14],
        [9, 8, 0, 11, 10, 6, 3, 9, 5, 8, 4, 15, 14, 13, 9, 18, 9],
        [8, 3, 11, 0, 1, 7, 10, 6, 10, 10, 14, 6, 7, 9, 14, 6, 16],
        [7, 2, 10, 1, 0, 6, 9, 4, 8, 9, 13, 4, 6, 8, 12, 8, 14],
        [3, 6, 6, 7, 6, 0, 2, 3, 2, 2, 7, 9, 7, 7, 6, 12, 8],
        [6, 8, 3, 10, 9, 2, 0, 6, 2, 5, 4, 12, 10, 10, 6, 15, 5],
        [2, 4, 9, 6, 4, 3, 6, 0, 4, 4, 8, 5, 4, 3, 7, 8, 10],
        [3, 8, 5, 10, 8, 2, 2, 4, 0, 3, 4, 9, 8, 7, 3, 13, 6],
        [2, 8, 8, 10, 9, 2, 5, 4, 3, 0, 4, 6, 5, 4, 3, 9, 5],
        [6, 13, 4, 14, 13, 7, 4, 8, 4, 4, 0, 10, 9, 8, 4, 13, 4],
        [6, 7, 15, 6, 4, 9, 12, 5, 9, 6, 10, 0, 1, 3, 7, 3, 10],
        [4, 5, 14, 7, 6, 7, 10, 4, 8, 5, 9, 1, 0, 2, 6, 4, 8],
        [4, 8, 13, 9, 8, 7, 10, 3, 7, 4, 8, 3, 2, 0, 4, 5, 6],
        [5, 12, 9, 14, 12, 6, 6, 7, 3, 3, 4, 7, 6, 4, 0, 9, 2],
        [9, 10, 18, 6, 8, 12, 15, 8, 13, 9, 13, 3, 4, 5, 9, 0, 9],
        [7, 14, 9, 16, 14, 8, 5, 10, 6, 5, 4, 10, 8, 6, 2, 9, 0],
    ]
    data['time_windows'] = [
        (0, 5),  # depot
        (7, 12),  # 1
        (10, 15),  # 2
        (16, 18),  # 3
        (10, 13),  # 4
        (0, 5),  # 5
        (5, 10),  # 6
        (0, 4),  # 7
        (5, 10),  # 8
        (0, 3),  # 9
        (10, 16),  # 10
        (10, 15),  # 11
        (0, 5),  # 12
        (5, 10),  # 13
        (7, 8),  # 14
        (10, 15),  # 15
        (11, 15),  # 16
    ]
    data['num_vehicles'] = 4
    data['depot'] = 0
    return data


def print_solution(data, manager, routing, solution):
    """Prints solution on console."""
    print(f'Objective: {solution.ObjectiveValue()}')
    time_dimension = routing.GetDimensionOrDie('Time')
    total_time = 0
    for vehicle_id in range(data['num_vehicles']):
        index = routing.Start(vehicle_id)
        plan_output = 'Route for vehicle {}:n'.format(vehicle_id)
        while not routing.IsEnd(index):
            time_var = time_dimension.CumulVar(index)
            plan_output += '{0} Time({1},{2}) -> '.format(
                manager.IndexToNode(index), solution.Min(time_var),
                solution.Max(time_var))
            index = solution.Value(routing.NextVar(index))
        time_var = time_dimension.CumulVar(index)
        plan_output += '{0} Time({1},{2})n'.format(manager.IndexToNode(index),
                                                    solution.Min(time_var),
                                                    solution.Max(time_var))
        plan_output += 'Time of the route: {}minn'.format(
            solution.Min(time_var))
        print(plan_output)
        total_time += solution.Min(time_var)
    print('Total time of all routes: {}min'.format(total_time))


def main():
    """Solve the VRP with time windows."""
    # Instantiate the data problem.
    data = create_data_model()

    # Create the routing index manager.
    manager = pywrapcp.RoutingIndexManager(len(data['time_matrix']),
                                           data['num_vehicles'], data['depot'])

    # Create Routing Model.
    routing = pywrapcp.RoutingModel(manager)


    # Create and register a transit callback.
    def time_callback(from_index, to_index):
        """Returns the travel time between the two nodes."""
        # Convert from routing variable Index to time matrix NodeIndex.
        from_node = manager.IndexToNode(from_index)
        to_node = manager.IndexToNode(to_index)
        return data['time_matrix'][from_node][to_node]

    transit_callback_index = routing.RegisterTransitCallback(time_callback)

    # Define cost of each arc.
    routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)

    # Add Time Windows constraint.
    time = 'Time'
    routing.AddDimension(
        transit_callback_index,
        30,  # allow waiting time
        30,  # maximum time per vehicle
        False,  # Don't force start cumul to zero.
        time)
    time_dimension = routing.GetDimensionOrDie(time)
    # Add time window constraints for each location except depot.
    for location_idx, time_window in enumerate(data['time_windows']):
        if location_idx == data['depot']:
            continue
        index = manager.NodeToIndex(location_idx)
        time_dimension.CumulVar(index).SetRange(time_window[0], time_window[1])
    # Add time window constraints for each vehicle start node.
    depot_idx = data['depot']
    for vehicle_id in range(data['num_vehicles']):
        index = routing.Start(vehicle_id)
        time_dimension.CumulVar(index).SetRange(
            data['time_windows'][depot_idx][0],
            data['time_windows'][depot_idx][1])

    # Instantiate route start and end times to produce feasible times.
    for i in range(data['num_vehicles']):
        routing.AddVariableMinimizedByFinalizer(
            time_dimension.CumulVar(routing.Start(i)))
        routing.AddVariableMinimizedByFinalizer(
            time_dimension.CumulVar(routing.End(i)))

    # Setting first solution heuristic.
    search_parameters = pywrapcp.DefaultRoutingSearchParameters()
    search_parameters.first_solution_strategy = (
        routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC)

    # Solve the problem.
    solution = routing.SolveWithParameters(search_parameters)

    # Print solution on console.
    if solution:
        print_solution(data, manager, routing, solution)


if __name__ == '__main__':
    main()

C++

#include <cstdint>
#include <sstream>
#include <string>
#include <utility>
#include <vector>

#include "ortools/constraint_solver/routing.h"
#include "ortools/constraint_solver/routing_enums.pb.h"
#include "ortools/constraint_solver/routing_index_manager.h"
#include "ortools/constraint_solver/routing_parameters.h"

namespace operations_research {
struct DataModel {
  const std::vector<std::vector<int64_t>> time_matrix{
      {0, 6, 9, 8, 7, 3, 6, 2, 3, 2, 6, 6, 4, 4, 5, 9, 7},
      {6, 0, 8, 3, 2, 6, 8, 4, 8, 8, 13, 7, 5, 8, 12, 10, 14},
      {9, 8, 0, 11, 10, 6, 3, 9, 5, 8, 4, 15, 14, 13, 9, 18, 9},
      {8, 3, 11, 0, 1, 7, 10, 6, 10, 10, 14, 6, 7, 9, 14, 6, 16},
      {7, 2, 10, 1, 0, 6, 9, 4, 8, 9, 13, 4, 6, 8, 12, 8, 14},
      {3, 6, 6, 7, 6, 0, 2, 3, 2, 2, 7, 9, 7, 7, 6, 12, 8},
      {6, 8, 3, 10, 9, 2, 0, 6, 2, 5, 4, 12, 10, 10, 6, 15, 5},
      {2, 4, 9, 6, 4, 3, 6, 0, 4, 4, 8, 5, 4, 3, 7, 8, 10},
      {3, 8, 5, 10, 8, 2, 2, 4, 0, 3, 4, 9, 8, 7, 3, 13, 6},
      {2, 8, 8, 10, 9, 2, 5, 4, 3, 0, 4, 6, 5, 4, 3, 9, 5},
      {6, 13, 4, 14, 13, 7, 4, 8, 4, 4, 0, 10, 9, 8, 4, 13, 4},
      {6, 7, 15, 6, 4, 9, 12, 5, 9, 6, 10, 0, 1, 3, 7, 3, 10},
      {4, 5, 14, 7, 6, 7, 10, 4, 8, 5, 9, 1, 0, 2, 6, 4, 8},
      {4, 8, 13, 9, 8, 7, 10, 3, 7, 4, 8, 3, 2, 0, 4, 5, 6},
      {5, 12, 9, 14, 12, 6, 6, 7, 3, 3, 4, 7, 6, 4, 0, 9, 2},
      {9, 10, 18, 6, 8, 12, 15, 8, 13, 9, 13, 3, 4, 5, 9, 0, 9},
      {7, 14, 9, 16, 14, 8, 5, 10, 6, 5, 4, 10, 8, 6, 2, 9, 0},
  };
  const std::vector<std::pair<int64_t, int64_t>> time_windows{
      {0, 5},    // depot
      {7, 12},   // 1
      {10, 15},  // 2
      {16, 18},  // 3
      {10, 13},  // 4
      {0, 5},    // 5
      {5, 10},   // 6
      {0, 4},    // 7
      {5, 10},   // 8
      {0, 3},    // 9
      {10, 16},  // 10
      {10, 15},  // 11
      {0, 5},    // 12
      {5, 10},   // 13
      {7, 8},    // 14
      {10, 15},  // 15
      {11, 15},  // 16
  };
  const int num_vehicles = 4;
  const RoutingIndexManager::NodeIndex depot{0};
};

//! @brief Print the solution.
//! @param[in] data Data of the problem.
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const DataModel& data, const RoutingIndexManager& manager,
                   const RoutingModel& routing, const Assignment& solution) {
  const RoutingDimension& time_dimension = routing.GetDimensionOrDie("Time");
  int64_t total_time{0};
  for (int vehicle_id = 0; vehicle_id < data.num_vehicles; ++vehicle_id) {
    int64_t index = routing.Start(vehicle_id);
    LOG(INFO) << "Route for vehicle " << vehicle_id << ":";
    std::ostringstream route;
    while (routing.IsEnd(index) == false) {
      auto time_var = time_dimension.CumulVar(index);
      route << manager.IndexToNode(index).value() << " Time("
            << solution.Min(time_var) << ", " << solution.Max(time_var)
            << ") -> ";
      index = solution.Value(routing.NextVar(index));
    }
    auto time_var = time_dimension.CumulVar(index);
    LOG(INFO) << route.str() << manager.IndexToNode(index).value() << " Time("
              << solution.Min(time_var) << ", " << solution.Max(time_var)
              << ")";
    LOG(INFO) << "Time of the route: " << solution.Min(time_var) << "min";
    total_time += solution.Min(time_var);
  }
  LOG(INFO) << "Total time of all routes: " << total_time << "min";
  LOG(INFO) << "";
  LOG(INFO) << "Advanced usage:";
  LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}

void VrpTimeWindows() {
  // Instantiate the data problem.
  DataModel data;

  // Create Routing Index Manager
  RoutingIndexManager manager(data.time_matrix.size(), data.num_vehicles,
                              data.depot);

  // Create Routing Model.
  RoutingModel routing(manager);

  // Create and register a transit callback.
  const int transit_callback_index = routing.RegisterTransitCallback(
      [&data, &manager](int64_t from_index, int64_t to_index) -> int64_t {
        // Convert from routing variable Index to time matrix NodeIndex.
        auto from_node = manager.IndexToNode(from_index).value();
        auto to_node = manager.IndexToNode(to_index).value();
        return data.time_matrix[from_node][to_node];
      });

  // Define cost of each arc.
  routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);

  // Add Time constraint.
  std::string time{"Time"};
  routing.AddDimension(transit_callback_index,  // transit callback index
                       int64_t{30},             // allow waiting time
                       int64_t{30},             // maximum time per vehicle
                       false,  // Don't force start cumul to zero
                       time);
  const RoutingDimension& time_dimension = routing.GetDimensionOrDie(time);
  // Add time window constraints for each location except depot.
  for (int i = 1; i < data.time_windows.size(); ++i) {
    int64_t index = manager.NodeToIndex(RoutingIndexManager::NodeIndex(i));
    time_dimension.CumulVar(index)->SetRange(data.time_windows[i].first,
                                             data.time_windows[i].second);
  }
  // Add time window constraints for each vehicle start node.
  for (int i = 0; i < data.num_vehicles; ++i) {
    int64_t index = routing.Start(i);
    time_dimension.CumulVar(index)->SetRange(data.time_windows[0].first,
                                             data.time_windows[0].second);
  }

  // Instantiate route start and end times to produce feasible times.
  for (int i = 0; i < data.num_vehicles; ++i) {
    routing.AddVariableMinimizedByFinalizer(
        time_dimension.CumulVar(routing.Start(i)));
    routing.AddVariableMinimizedByFinalizer(
        time_dimension.CumulVar(routing.End(i)));
  }

  // Setting first solution heuristic.
  RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
  searchParameters.set_first_solution_strategy(
      FirstSolutionStrategy::PATH_CHEAPEST_ARC);

  // Solve the problem.
  const Assignment* solution = routing.SolveWithParameters(searchParameters);

  // Print solution on console.
  PrintSolution(data, manager, routing, *solution);
}
}  // namespace operations_research

int main(int /*argc*/, char* /*argv*/[]) {
  operations_research::VrpTimeWindows();
  return EXIT_SUCCESS;
}

Java

package com.google.ortools.constraintsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.Assignment;
import com.google.ortools.constraintsolver.FirstSolutionStrategy;
import com.google.ortools.constraintsolver.IntVar;
import com.google.ortools.constraintsolver.RoutingDimension;
import com.google.ortools.constraintsolver.RoutingIndexManager;
import com.google.ortools.constraintsolver.RoutingModel;
import com.google.ortools.constraintsolver.RoutingSearchParameters;
import com.google.ortools.constraintsolver.main;
import java.util.logging.Logger;

/** VRPTW. */
public class VrpTimeWindows {
  private static final Logger logger = Logger.getLogger(VrpTimeWindows.class.getName());
  static class DataModel {
    public final long[][] timeMatrix = {
        {0, 6, 9, 8, 7, 3, 6, 2, 3, 2, 6, 6, 4, 4, 5, 9, 7},
        {6, 0, 8, 3, 2, 6, 8, 4, 8, 8, 13, 7, 5, 8, 12, 10, 14},
        {9, 8, 0, 11, 10, 6, 3, 9, 5, 8, 4, 15, 14, 13, 9, 18, 9},
        {8, 3, 11, 0, 1, 7, 10, 6, 10, 10, 14, 6, 7, 9, 14, 6, 16},
        {7, 2, 10, 1, 0, 6, 9, 4, 8, 9, 13, 4, 6, 8, 12, 8, 14},
        {3, 6, 6, 7, 6, 0, 2, 3, 2, 2, 7, 9, 7, 7, 6, 12, 8},
        {6, 8, 3, 10, 9, 2, 0, 6, 2, 5, 4, 12, 10, 10, 6, 15, 5},
        {2, 4, 9, 6, 4, 3, 6, 0, 4, 4, 8, 5, 4, 3, 7, 8, 10},
        {3, 8, 5, 10, 8, 2, 2, 4, 0, 3, 4, 9, 8, 7, 3, 13, 6},
        {2, 8, 8, 10, 9, 2, 5, 4, 3, 0, 4, 6, 5, 4, 3, 9, 5},
        {6, 13, 4, 14, 13, 7, 4, 8, 4, 4, 0, 10, 9, 8, 4, 13, 4},
        {6, 7, 15, 6, 4, 9, 12, 5, 9, 6, 10, 0, 1, 3, 7, 3, 10},
        {4, 5, 14, 7, 6, 7, 10, 4, 8, 5, 9, 1, 0, 2, 6, 4, 8},
        {4, 8, 13, 9, 8, 7, 10, 3, 7, 4, 8, 3, 2, 0, 4, 5, 6},
        {5, 12, 9, 14, 12, 6, 6, 7, 3, 3, 4, 7, 6, 4, 0, 9, 2},
        {9, 10, 18, 6, 8, 12, 15, 8, 13, 9, 13, 3, 4, 5, 9, 0, 9},
        {7, 14, 9, 16, 14, 8, 5, 10, 6, 5, 4, 10, 8, 6, 2, 9, 0},
    };
    public final long[][] timeWindows = {
        {0, 5}, // depot
        {7, 12}, // 1
        {10, 15}, // 2
        {16, 18}, // 3
        {10, 13}, // 4
        {0, 5}, // 5
        {5, 10}, // 6
        {0, 4}, // 7
        {5, 10}, // 8
        {0, 3}, // 9
        {10, 16}, // 10
        {10, 15}, // 11
        {0, 5}, // 12
        {5, 10}, // 13
        {7, 8}, // 14
        {10, 15}, // 15
        {11, 15}, // 16
    };
    public final int vehicleNumber = 4;
    public final int depot = 0;
  }

  /// @brief Print the solution.
  static void printSolution(
      DataModel data, RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
    // Solution cost.
    logger.info("Objective : " + solution.objectiveValue());
    // Inspect solution.
    RoutingDimension timeDimension = routing.getMutableDimension("Time");
    long totalTime = 0;
    for (int i = 0; i < data.vehicleNumber; ++i) {
      long index = routing.start(i);
      logger.info("Route for Vehicle " + i + ":");
      String route = "";
      while (!routing.isEnd(index)) {
        IntVar timeVar = timeDimension.cumulVar(index);
        route += manager.indexToNode(index) + " Time(" + solution.min(timeVar) + ","
            + solution.max(timeVar) + ") -> ";
        index = solution.value(routing.nextVar(index));
      }
      IntVar timeVar = timeDimension.cumulVar(index);
      route += manager.indexToNode(index) + " Time(" + solution.min(timeVar) + ","
          + solution.max(timeVar) + ")";
      logger.info(route);
      logger.info("Time of the route: " + solution.min(timeVar) + "min");
      totalTime += solution.min(timeVar);
    }
    logger.info("Total time of all routes: " + totalTime + "min");
  }

  public static void main(String[] args) throws Exception {
    Loader.loadNativeLibraries();
    // Instantiate the data problem.
    final DataModel data = new DataModel();

    // Create Routing Index Manager
    RoutingIndexManager manager =
        new RoutingIndexManager(data.timeMatrix.length, data.vehicleNumber, data.depot);

    // Create Routing Model.
    RoutingModel routing = new RoutingModel(manager);

    // Create and register a transit callback.
    final int transitCallbackIndex =
        routing.registerTransitCallback((long fromIndex, long toIndex) -> {
          // Convert from routing variable Index to user NodeIndex.
          int fromNode = manager.indexToNode(fromIndex);
          int toNode = manager.indexToNode(toIndex);
          return data.timeMatrix[fromNode][toNode];
        });

    // Define cost of each arc.
    routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);

    // Add Time constraint.
    routing.addDimension(transitCallbackIndex, // transit callback
        30, // allow waiting time
        30, // vehicle maximum capacities
        false, // start cumul to zero
        "Time");
    RoutingDimension timeDimension = routing.getMutableDimension("Time");
    // Add time window constraints for each location except depot.
    for (int i = 1; i < data.timeWindows.length; ++i) {
      long index = manager.nodeToIndex(i);
      timeDimension.cumulVar(index).setRange(data.timeWindows[i][0], data.timeWindows[i][1]);
    }
    // Add time window constraints for each vehicle start node.
    for (int i = 0; i < data.vehicleNumber; ++i) {
      long index = routing.start(i);
      timeDimension.cumulVar(index).setRange(data.timeWindows[0][0], data.timeWindows[0][1]);
    }

    // Instantiate route start and end times to produce feasible times.
    for (int i = 0; i < data.vehicleNumber; ++i) {
      routing.addVariableMinimizedByFinalizer(timeDimension.cumulVar(routing.start(i)));
      routing.addVariableMinimizedByFinalizer(timeDimension.cumulVar(routing.end(i)));
    }

    // Setting first solution heuristic.
    RoutingSearchParameters searchParameters =
        main.defaultRoutingSearchParameters()
            .toBuilder()
            .setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
            .build();

    // Solve the problem.
    Assignment solution = routing.solveWithParameters(searchParameters);

    // Print solution on console.
    printSolution(data, routing, manager, solution);
  }
}
// [END_program_part1]

C#

using System;
using System.Collections.Generic;
using Google.OrTools.ConstraintSolver;

/// <summary>
///   Vehicles Routing Problem (VRP) with Time Windows.
/// </summary>
public class VrpTimeWindows
{
    class DataModel
    {
        public long[,] TimeMatrix = {
            { 0, 6, 9, 8, 7, 3, 6, 2, 3, 2, 6, 6, 4, 4, 5, 9, 7 },
            { 6, 0, 8, 3, 2, 6, 8, 4, 8, 8, 13, 7, 5, 8, 12, 10, 14 },
            { 9, 8, 0, 11, 10, 6, 3, 9, 5, 8, 4, 15, 14, 13, 9, 18, 9 },
            { 8, 3, 11, 0, 1, 7, 10, 6, 10, 10, 14, 6, 7, 9, 14, 6, 16 },
            { 7, 2, 10, 1, 0, 6, 9, 4, 8, 9, 13, 4, 6, 8, 12, 8, 14 },
            { 3, 6, 6, 7, 6, 0, 2, 3, 2, 2, 7, 9, 7, 7, 6, 12, 8 },
            { 6, 8, 3, 10, 9, 2, 0, 6, 2, 5, 4, 12, 10, 10, 6, 15, 5 },
            { 2, 4, 9, 6, 4, 3, 6, 0, 4, 4, 8, 5, 4, 3, 7, 8, 10 },
            { 3, 8, 5, 10, 8, 2, 2, 4, 0, 3, 4, 9, 8, 7, 3, 13, 6 },
            { 2, 8, 8, 10, 9, 2, 5, 4, 3, 0, 4, 6, 5, 4, 3, 9, 5 },
            { 6, 13, 4, 14, 13, 7, 4, 8, 4, 4, 0, 10, 9, 8, 4, 13, 4 },
            { 6, 7, 15, 6, 4, 9, 12, 5, 9, 6, 10, 0, 1, 3, 7, 3, 10 },
            { 4, 5, 14, 7, 6, 7, 10, 4, 8, 5, 9, 1, 0, 2, 6, 4, 8 },
            { 4, 8, 13, 9, 8, 7, 10, 3, 7, 4, 8, 3, 2, 0, 4, 5, 6 },
            { 5, 12, 9, 14, 12, 6, 6, 7, 3, 3, 4, 7, 6, 4, 0, 9, 2 },
            { 9, 10, 18, 6, 8, 12, 15, 8, 13, 9, 13, 3, 4, 5, 9, 0, 9 },
            { 7, 14, 9, 16, 14, 8, 5, 10, 6, 5, 4, 10, 8, 6, 2, 9, 0 },
        };
        public long[,] TimeWindows = {
            { 0, 5 },   // depot
            { 7, 12 },  // 1
            { 10, 15 }, // 2
            { 16, 18 }, // 3
            { 10, 13 }, // 4
            { 0, 5 },   // 5
            { 5, 10 },  // 6
            { 0, 4 },   // 7
            { 5, 10 },  // 8
            { 0, 3 },   // 9
            { 10, 16 }, // 10
            { 10, 15 }, // 11
            { 0, 5 },   // 12
            { 5, 10 },  // 13
            { 7, 8 },   // 14
            { 10, 15 }, // 15
            { 11, 15 }, // 16
        };
        public int VehicleNumber = 4;
        public int Depot = 0;
    };

    /// <summary>
    ///   Print the solution.
    /// </summary>
    static void PrintSolution(in DataModel data, in RoutingModel routing, in RoutingIndexManager manager,
                              in Assignment solution)
    {
        Console.WriteLine($"Objective {solution.ObjectiveValue()}:");

        // Inspect solution.
        RoutingDimension timeDimension = routing.GetMutableDimension("Time");
        long totalTime = 0;
        for (int i = 0; i < data.VehicleNumber; ++i)
        {
            Console.WriteLine("Route for Vehicle {0}:", i);
            var index = routing.Start(i);
            while (routing.IsEnd(index) == false)
            {
                var timeVar = timeDimension.CumulVar(index);
                Console.Write("{0} Time({1},{2}) -> ", manager.IndexToNode(index), solution.Min(timeVar),
                              solution.Max(timeVar));
                index = solution.Value(routing.NextVar(index));
            }
            var endTimeVar = timeDimension.CumulVar(index);
            Console.WriteLine("{0} Time({1},{2})", manager.IndexToNode(index), solution.Min(endTimeVar),
                              solution.Max(endTimeVar));
            Console.WriteLine("Time of the route: {0}min", solution.Min(endTimeVar));
            totalTime += solution.Min(endTimeVar);
        }
        Console.WriteLine("Total time of all routes: {0}min", totalTime);
    }

    public static void Main(String[] args)
    {
        // Instantiate the data problem.
        DataModel data = new DataModel();

        // Create Routing Index Manager
        RoutingIndexManager manager =
            new RoutingIndexManager(data.TimeMatrix.GetLength(0), data.VehicleNumber, data.Depot);

        // Create Routing Model.
        RoutingModel routing = new RoutingModel(manager);

        // Create and register a transit callback.
        int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
                                                                   {
                                                                       // Convert from routing variable Index to time
                                                                       // matrix NodeIndex.
                                                                       var fromNode = manager.IndexToNode(fromIndex);
                                                                       var toNode = manager.IndexToNode(toIndex);
                                                                       return data.TimeMatrix[fromNode, toNode];
                                                                   });

        // Define cost of each arc.
        routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);

        // Add Time constraint.
        routing.AddDimension(transitCallbackIndex, // transit callback
                             30,                   // allow waiting time
                             30,                   // vehicle maximum capacities
                             false,                // start cumul to zero
                             "Time");
        RoutingDimension timeDimension = routing.GetMutableDimension("Time");
        // Add time window constraints for each location except depot.
        for (int i = 1; i < data.TimeWindows.GetLength(0); ++i)
        {
            long index = manager.NodeToIndex(i);
            timeDimension.CumulVar(index).SetRange(data.TimeWindows[i, 0], data.TimeWindows[i, 1]);
        }
        // Add time window constraints for each vehicle start node.
        for (int i = 0; i < data.VehicleNumber; ++i)
        {
            long index = routing.Start(i);
            timeDimension.CumulVar(index).SetRange(data.TimeWindows[0, 0], data.TimeWindows[0, 1]);
        }

        // Instantiate route start and end times to produce feasible times.
        for (int i = 0; i < data.VehicleNumber; ++i)
        {
            routing.AddVariableMinimizedByFinalizer(timeDimension.CumulVar(routing.Start(i)));
            routing.AddVariableMinimizedByFinalizer(timeDimension.CumulVar(routing.End(i)));
        }

        // Setting first solution heuristic.
        RoutingSearchParameters searchParameters =
            operations_research_constraint_solver.DefaultRoutingSearchParameters();
        searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;

        // Solve the problem.
        Assignment solution = routing.SolveWithParameters(searchParameters);

        // Print solution on console.
        PrintSolution(data, routing, manager, solution);
    }
}

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License, and code samples are licensed under the Apache 2.0 License. For details, see the Google Developers Site Policies. Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-16 UTC.

Источник

Principles learned¶

Add multiple list decision variables
Use lambda expressions to define a recursive array

Define a sequence of expressions

Problem¶

In the capacitated vehicle routing problem with time-windows (CVRPTW),
a fleet of delivery vehicles with uniform capacity must service customers
with known demand and opening hours for a single commodity.
The vehicles start and end their routes at a common depot.
Each customer can only be served by one vehicle. The objectives are
to minimize the fleet size and assign a sequence of customers to each truck
of the fleet minimizing the total distance traveled such that all customers
are served and the total demand served by each truck does not exceed its
capacity.

Download the example

Data¶

The instances provided come from the Solomon instances.

The format of the data files is as follows:

The first line gives the name of the instance
The fifth line contains the number of vehicles and their common capacity
From the 10th line, each line contains the integer data associated to each
customer, starting with the depot:
- The index of the customer
- The x coordinate
- The y coordinate
- The demand
- The earliest arrival
- The latest arrival
- The service time

Program¶

The LocalSolver model is an extension of the CVRP model.
We refer the reader to this model for the routing aspect of the problem.
The time-windows are handled as a prioritary objective. In case of early
arrival, the truck has to wait for the opening hour of the customer. In case of
late arrival, the lateness is measured and the total lateness has to be
minimized. The solution is feasible when this cumulated lateness is zero.

In the model the ending times of each truck are defined as a recursive array.
The arrival time is the maximum of:

the end time of the previous visit plus the traveling time (equal to the
distance in these instances). For the first visit it amounts to the traveling
time from the depot (starting at t=0)
the earliest allowed arrival at this customer

The ending time is merely this arrival time plus the service time for this
customer. The arrival to the depot at the end of the tour occurs at the end time
of the last visit plus the traveling time from this point to the depot.

Such a recursive definition is introduced with a function (i, prev) => ....
It allows defining the ith element of an array in function of i and of the
(i-1)th element of the array. See our
documentation on this topic for details.

The lateness at each visit is computed from the difference between the ending
time of this visit and the latest allowed end for this customer. For the arrival
at the depot, we compare the arrival time to the maximum horizon defined for the
problem.

Finally we minimize in lexicographic order: the total lateness, the number of
trucks used, and the total distance traveled by all the trucks.

Execution:: localsolver cvrptw.lsp inFileName=instances/R101.25.txt [lsTimeLimit=] [solFileName=]

use io;

/* Read instance data. The input files follow the "Solomon" format*/
function input() {
    usage = "Usage: localsolver cvrptw.lsp "
            + "inFileName=inputFile [solFileName=outputFile] [lsTimeLimit=timeLimit]";

    if (inFileName == nil) throw usage;

    readInputCvrptw();

    computeDistanceMatrix();
}

/* Declare the optimization model */
function model() {
    customersSequences[k in 1..nbTrucks] <- list(nbCustomers);

    // All customers must be visited by the trucks
    constraint partition[k in 1..nbTrucks](customersSequences[k]);

    for [k in 1..nbTrucks] {
        local sequence <- customersSequences[k];
        local c <- count(sequence);

        // A truck is used if it visits at least one customer
        truckUsed[k] <- c > 0;

        // The quantity needed in each route must not exceed the truck capacity
        routeQuantity[k] <- sum(0..c-1, i => demands[sequence[i]]);
        constraint routeQuantity[k] <= truckCapacity;

        // End of each visit
        endTime[k] <- array(0..c-1, (i, prev) => max(earliestStart[sequence[i]],
                i == 0 ?
                distanceDepot[sequence[0]] :
                prev + distanceMatrix[sequence[i - 1]][sequence[i]]) + serviceTime[sequence[i]]);

        // Arriving home after max horizon
        homeLateness[k] <- truckUsed[k] ?
                max(0, endTime[k][c - 1] + distanceDepot[sequence[c - 1]] - maxHorizon) :
                0;

        // Distance traveled by truck k
        routeDistances[k] <- sum(1..c-1,
                i => distanceMatrix[sequence[i-1]][sequence[i]]) 
                + (truckUsed[k] ?
                (distanceDepot[sequence[0]] + distanceDepot[sequence[c - 1]]) :
                0);

        // Completing visit after latest end
        lateness[k] <- homeLateness[k] + sum(0..c-1,
                i => max(0, endTime[k][i] - latestEnd[sequence[i]]));
    }

    // Total lateness, must be 0 for a solution to be valid
    totalLateness <- sum[k in 1..nbTrucks](lateness[k]);

    // Total nb trucks used
    nbTrucksUsed <- sum[k in 1..nbTrucks](truckUsed[k]);

    // Total distance traveled (convention in Solomon's instances is to round to 2 decimals)
    totalDistance <- round(100 * sum[k in 1..nbTrucks](routeDistances[k])) / 100;

    // Objective: minimize the lateness, then the number of trucks used, then the distance traveled
    minimize totalLateness;
    minimize nbTrucksUsed;
    minimize totalDistance;
}


/* Parametrize the solver */
function param() {
    if (lsTimeLimit == nil) lsTimeLimit = 20;
}

/* Write the solution in a file with the following format:
 * - number of trucks used and total distance
 * - for each truck the customers visited (omitting the start/end at the depot) */
function output() {
    if (solFileName == nil) return;
    local outfile = io.openWrite(solFileName);

    outfile.println(nbTrucksUsed.value, " ", totalDistance.value);
    for [k in 1..nbTrucks] {
        if (truckUsed[k].value != 1) continue;
        for [customer in customersSequences[k].value] {
            outfile.print(customer + 1, " ");
        }
        outfile.println();
    }
}

function readInputCvrptw() {
    local inFile = io.openRead(inFileName);
    skipLines(inFile, 4);

    // Truck related data
    nbTrucks = inFile.readInt();
    truckCapacity = inFile.readInt();

    skipLines(inFile, 3);

    // Depot data
    local line = inFile.readln().split();
    depotIndex = line[0].toInt();
    depotX = line[1].toInt();
    depotY = line[2].toInt();
    maxHorizon = line[5].toInt();

    // Customers data
    i = 0;
    while (!inFile.eof()) {
        inLine = inFile.readln();
        line = inLine.split();
        if (count(line) == 0) break;
        if (count(line) != 7) throw "Wrong file format";
        customerIndex[i] = line[0].toInt();
        customerX[i] = line[1].toInt();
        customerY[i] = line[2].toInt();
        demands[i] = line[3].toInt();
        serviceTime[i] = line[6].toInt();
        earliestStart[i] = line[4].toInt();
        // in input files due date is meant as latest start time
        latestEnd[i] = line[5].toInt() + serviceTime[i];
        i = i + 1;
    }
    nbCustomers = i;

    inFile.close();
}

function skipLines(inFile, nbLines) {
    if (nbLines < 1) return;
    for [i in 1..nbLines] inFile.readln();
}

// Compute the distance matrix
function computeDistanceMatrix() {
    for [i in 0..nbCustomers-1] {
        distanceMatrix[i][i] = 0;
        for [j in i+1..nbCustomers-1] {
            local localDistance = computeDist(i, j);
            distanceMatrix[j][i] = localDistance;
            distanceMatrix[i][j] = localDistance;
        }
    }

    for [i in 0..nbCustomers-1] {
        local localDistance = computeDepotDist(i);
        distanceDepot[i] = localDistance;
    }
}

function computeDist(i, j) {
    local x1 = customerX[i];
    local x2 = customerX[j];
    local y1 = customerY[i];
    local y2 = customerY[j];
    return computeDistance(x1, x2, y1, y2);
}

function computeDepotDist(i) {
    local x1 = customerX[i];
    local xd = depotX;
    local y1 = customerY[i];
    local yd = depotY;
    return computeDistance(x1, xd, y1, yd);
}

function computeDistance(x1, x2, y1, y2) {
    return sqrt(pow((x1 - x2), 2) + pow((y1 - y2), 2));
}

Execution (Windows): set PYTHONPATH=%LS_HOME%binpython

python cvrptw.py instancesR101.25.txt

Execution (Linux): export PYTHONPATH=/opt/localsolver_11_5/bin/python

python cvrptw.py instances/R101.25.txt

import localsolver
import sys
import math


def read_elem(filename):
    with open(filename) as f:
        return [str(elem) for elem in f.read().split()]


def main(instance_file, str_time_limit, output_file):
    #
    # Read instance data
    #
    nb_customers, nb_trucks, truck_capacity, dist_matrix_data, dist_depot_data, 
        demands_data, service_time_data, earliest_start_data, latest_end_data, 
        max_horizon = read_input_cvrptw(instance_file)

    with localsolver.LocalSolver() as ls:
        #
        # Declare the optimization model
        #
        model = ls.model

        # Sequence of customers visited by each truck
        customers_sequences = [model.list(nb_customers) for k in range(nb_trucks)]

        # All customers must be visited by the trucks
        model.constraint(model.partition(customers_sequences))

        # Create LocalSolver arrays to be able to access them with an "at" operator
        demands = model.array(demands_data)
        earliest = model.array(earliest_start_data)
        latest = model.array(latest_end_data)
        service_time = model.array(service_time_data)
        dist_matrix = model.array()
        for n in range(nb_customers):
            dist_matrix.add_operand(model.array(dist_matrix_data[n]))
        dist_depot = model.array(dist_depot_data)

        dist_routes = [None] * nb_trucks
        end_time = [None] * nb_trucks
        home_lateness = [None] * nb_trucks
        lateness = [None] * nb_trucks

        # A truck is used if it visits at least one customer
        trucks_used = [(model.count(customers_sequences[k]) > 0) for k in range(nb_trucks)]
        nb_trucks_used = model.sum(trucks_used)

        for k in range(nb_trucks):
            sequence = customers_sequences[k]
            c = model.count(sequence)

            # The quantity needed in each route must not exceed the truck capacity
            demand_lambda = model.lambda_function(lambda i: demands[sequence[i]])
            route_quantity = model.sum(model.range(0, c), demand_lambda)
            model.constraint(route_quantity <= truck_capacity)

            # Distance traveled by each truck
            dist_lambda = model.lambda_function(
                lambda i: model.at(dist_matrix, sequence[i - 1], sequence[i]))
            dist_routes[k] = model.sum(model.range(1, c), dist_lambda) 
                + model.iif(c > 0, dist_depot[sequence[0]] + dist_depot[sequence[c - 1]], 0)

            # End of each visit
            end_time_lambda = model.lambda_function(
                lambda i, prev:
                    model.max(
                        earliest[sequence[i]],
                        model.iif(
                            i == 0, dist_depot[sequence[0]],
                            prev + model.at(dist_matrix, sequence[i - 1], sequence[i])))
                    + service_time[sequence[i]])

            end_time[k] = model.array(model.range(0, c), end_time_lambda)

            # Arriving home after max horizon
            home_lateness[k] = model.iif(
                trucks_used[k],
                model.max(
                    0,
                    end_time[k][c - 1] + dist_depot[sequence[c - 1]] - max_horizon),
                0)

            # Completing visit after latest end
            late_lambda = model.lambda_function(
                lambda i: model.max(0, end_time[k][i] - latest[sequence[i]]))
            lateness[k] = home_lateness[k] + model.sum(model.range(0, c), late_lambda)

        # Total lateness
        total_lateness = model.sum(lateness)

        # Total distance traveled
        total_distance = model.div(model.round(100 * model.sum(dist_routes)), 100)

        # Objective: minimize the number of trucks used, then minimize the distance traveled
        model.minimize(total_lateness)
        model.minimize(nb_trucks_used)
        model.minimize(total_distance)

        model.close()

        # Parameterize the solver
        ls.param.time_limit = int(str_time_limit)

        ls.solve()

        #
        # Write the solution in a file with the following format:
        #  - number of trucks used and total distance
        #  - for each truck the customers visited (omitting the start/end at the depot)
        #
        if output_file is not None:
            with open(output_file, 'w') as f:
                f.write("%d %dn" % (nb_trucks_used.value, total_distance.value))
                for k in range(nb_trucks):
                    if trucks_used[k].value != 1:
                        continue
                    # Values in sequence are in [0..nbCustomers-1]. +1 is to put it back in
                    # [1..nbCustomers] as in the data files (0 being the depot)
                    for customer in customers_sequences[k].value:
                        f.write("%d " % (customer + 1))
                    f.write("n")


# The input files follow the "Solomon" format
def read_input_cvrptw(filename):
    file_it = iter(read_elem(filename))

    for i in range(4):
        next(file_it)

    nb_trucks = int(next(file_it))
    truck_capacity = int(next(file_it))

    for i in range(13):
        next(file_it)

    depot_x = int(next(file_it))
    depot_y = int(next(file_it))

    for i in range(2):
        next(file_it)

    max_horizon = int(next(file_it))

    next(file_it)

    customers_x = []
    customers_y = []
    demands = []
    earliest_start = []
    latest_end = []
    service_time = []

    while True:
        val = next(file_it, None)
        if val is None:
            break
        i = int(val) - 1
        customers_x.append(int(next(file_it)))
        customers_y.append(int(next(file_it)))
        demands.append(int(next(file_it)))
        ready = int(next(file_it))
        due = int(next(file_it))
        stime = int(next(file_it))
        earliest_start.append(ready)
        # in input files due date is meant as latest start time
        latest_end.append(due + stime)
        service_time.append(stime)

    nb_customers = i + 1

    # Compute distance matrix
    distance_matrix = compute_distance_matrix(customers_x, customers_y)
    distance_depots = compute_distance_depots(depot_x, depot_y, customers_x, customers_y)

    return nb_customers, nb_trucks, truck_capacity, distance_matrix, distance_depots, 
        demands, service_time, earliest_start, latest_end, max_horizon


# Computes the distance matrix
def compute_distance_matrix(customers_x, customers_y):
    nb_customers = len(customers_x)
    distance_matrix = [[None for i in range(nb_customers)] for j in range(nb_customers)]
    for i in range(nb_customers):
        distance_matrix[i][i] = 0
        for j in range(nb_customers):
            dist = compute_dist(customers_x[i], customers_x[j],
                                customers_y[i], customers_y[j])
            distance_matrix[i][j] = dist
            distance_matrix[j][i] = dist
    return distance_matrix


# Computes the distances to depot
def compute_distance_depots(depot_x, depot_y, customers_x, customers_y):
    nb_customers = len(customers_x)
    distance_depots = [None] * nb_customers
    for i in range(nb_customers):
        dist = compute_dist(depot_x, customers_x[i], depot_y, customers_y[i])
        distance_depots[i] = dist
    return distance_depots


def compute_dist(xi, xj, yi, yj):
    return math.sqrt(math.pow(xi - xj, 2) + math.pow(yi - yj, 2))


if __name__ == '__main__':
    if len(sys.argv) < 2:
        print("Usage: python cvrptw.py input_file [output_file] [time_limit]")
        sys.exit(1)

    instance_file = sys.argv[1]
    output_file = sys.argv[2] if len(sys.argv) > 2 else None
    str_time_limit = sys.argv[3] if len(sys.argv) > 3 else "20"

    main(instance_file, str_time_limit, output_file)

Compilation / Execution (Windows): cl /EHsc cvrptw.cpp -I%LS_HOME%include /link %LS_HOME%binlocalsolver115.lib

cvrptw instancesR101.25.txt

Compilation / Execution (Linux): g++ cvrptw.cpp -I/opt/localsolver_11_5/include -llocalsolver115 -lpthread -o cvrptw

./cvrptw instances/R101.25.txt

#include "localsolver.h"
#include <cmath>
#include <cstring>
#include <fstream>
#include <iostream>
#include <vector>

using namespace localsolver;
using namespace std;

class Cvrptw {
public:
    // LocalSolver
    LocalSolver localsolver;

    // Number of customers
    int nbCustomers;

    // Capacity of the trucks
    int truckCapacity;

    // Latest allowed arrival to depot
    int maxHorizon;

    // Demand on each node
    vector<int> demandsData;

    // Earliest arrival on each node
    vector<int> earliestStartData;

    // Latest departure from each node
    vector<int> latestEndData;

    // Service time on each node
    vector<int> serviceTimeData;

    // Distance matrix between customers
    vector<vector<double>> distMatrixData;

    // Distance  between customers and depot
    vector<double> distDepotData;

    // Number of trucks
    int nbTrucks;

    // Decision variables
    vector<LSExpression> customersSequences;

    // Are the trucks actually used
    vector<LSExpression> trucksUsed;

    // Cumulated lateness in the solution (must be 0 for the solution to be valid)
    LSExpression totalLateness;

    // Number of trucks used in the solution
    LSExpression nbTrucksUsed;

    // Distance traveled by all the trucks
    LSExpression totalDistance;

    Cvrptw() {}

    /* Read instance data */
    void readInstance(const string& fileName) { readInputCvrptw(fileName); }

    void solve(int limit) {
        // Declare the optimization model
        LSModel model = localsolver.getModel();

        // Sequence of customers visited by each truck
        customersSequences.resize(nbTrucks);
        for (int k = 0; k < nbTrucks; ++k) {
            customersSequences[k] = model.listVar(nbCustomers);
        }

        // All customers must be visited by the trucks
        model.constraint(model.partition(customersSequences.begin(), customersSequences.end()));

        // Create LocalSolver arrays to be able to access them with an "at" operator
        LSExpression demands = model.array(demandsData.begin(), demandsData.end());
        LSExpression earliest = model.array(earliestStartData.begin(), earliestStartData.end());
        LSExpression latest = model.array(latestEndData.begin(), latestEndData.end());
        LSExpression serviceTime = model.array(serviceTimeData.begin(), serviceTimeData.end());
        LSExpression distMatrix = model.array();
        for (int n = 0; n < nbCustomers; ++n) {
            distMatrix.addOperand(model.array(distMatrixData[n].begin(), distMatrixData[n].end()));
        }
        LSExpression distDepot = model.array(distDepotData.begin(), distDepotData.end());

        trucksUsed.resize(nbTrucks);
        vector<LSExpression> distRoutes(nbTrucks), endTime(nbTrucks), homeLateness(nbTrucks), lateness(nbTrucks);

        for (int k = 0; k < nbTrucks; ++k) {
            LSExpression sequence = customersSequences[k];
            LSExpression c = model.count(sequence);

            // A truck is used if it visits at least one customer
            trucksUsed[k] = c > 0;

            // The quantity needed in each route must not exceed the truck capacity
            LSExpression demandLambda =
                model.createLambdaFunction([&](LSExpression i) { return demands[sequence[i]]; });
            LSExpression routeQuantity = model.sum(model.range(0, c), demandLambda);
            model.constraint(routeQuantity <= truckCapacity);

            // Distance traveled by truck k
            LSExpression distLambda = model.createLambdaFunction(
                [&](LSExpression i) { return model.at(distMatrix, sequence[i - 1], sequence[i]); });
            distRoutes[k] = model.sum(model.range(1, c), distLambda) +
                            model.iif(c > 0, distDepot[sequence[0]] + distDepot[sequence[c - 1]], 0);

            // End of each visit
            LSExpression endTimeLambda = model.createLambdaFunction([&](LSExpression i, LSExpression prev) {
                return model.max(earliest[sequence[i]],
                                 model.iif(i == 0, distDepot[sequence[0]],
                                           prev + model.at(distMatrix, sequence[i - 1], sequence[i]))) +
                       serviceTime[sequence[i]];
            });

            endTime[k] = model.array(model.range(0, c), endTimeLambda);

            // Arriving home after max horizon
            homeLateness[k] =
                model.iif(trucksUsed[k], model.max(0, endTime[k][c - 1] + distDepot[sequence[c - 1]] - maxHorizon), 0);

            // Completing visit after latest end
            LSExpression lateLambda = model.createLambdaFunction(
                [&](LSExpression i) { return model.max(0, endTime[k][i] - latest[sequence[i]]); });
            lateness[k] = homeLateness[k] + model.sum(model.range(0, c), lateLambda);
        }

        // Total lateness
        totalLateness = model.sum(lateness.begin(), lateness.end());

        // Total nb trucks used
        nbTrucksUsed = model.sum(trucksUsed.begin(), trucksUsed.end());

        // Total distance traveled (convention in Solomon's instances is to round to 2 decimals)
        totalDistance = model.round(100 * model.sum(distRoutes.begin(), distRoutes.end())) / 100;

        // Objective: minimize the lateness, then the number of trucks used, then the distance traveled
        model.minimize(totalLateness);
        model.minimize(nbTrucksUsed);
        model.minimize(totalDistance);

        model.close();

        // Parametrize the solver
        localsolver.getParam().setTimeLimit(limit);

        localsolver.solve();
    }

    /* Write the solution in a file with the following format:
     *  - number of trucks used and total distance
     *  - for each truck the customers visited (omitting the start/end at the depot) */
    void writeSolution(const string& fileName) {
        ofstream outfile;
        outfile.exceptions(ofstream::failbit | ofstream::badbit);
        outfile.open(fileName.c_str());

        outfile << nbTrucksUsed.getValue() << " " << totalDistance.getDoubleValue() << endl;
        for (int k = 0; k < nbTrucks; ++k) {
            if (trucksUsed[k].getValue() != 1)
                continue;
            // Values in sequence are in [0..nbCustomers-1]. +1 is to put it back in [1..nbCustomers]
            // as in the data files (0 being the depot)
            LSCollection customersCollection = customersSequences[k].getCollectionValue();
            for (int i = 0; i < customersCollection.count(); ++i) {
                outfile << customersCollection[i] + 1 << " ";
            }
            outfile << endl;
        }
    }

private:
    // The input files follow the "Solomon" format
    void readInputCvrptw(const string& fileName) {
        ifstream infile(fileName.c_str());
        if (!infile.is_open()) {
            throw std::runtime_error("File cannot be opened.");
        }

        string str;
        long tmp;

        int depotX, depotY;
        vector<int> customersX;
        vector<int> customersY;

        getline(infile, str);
        getline(infile, str);
        getline(infile, str);
        getline(infile, str);

        infile >> nbTrucks;
        infile >> truckCapacity;

        getline(infile, str);
        getline(infile, str);
        getline(infile, str);
        getline(infile, str);

        infile >> tmp;
        infile >> depotX;
        infile >> depotY;
        infile >> tmp;
        infile >> tmp;
        infile >> maxHorizon;
        infile >> tmp;

        while (infile >> tmp) {
            int cx, cy, demand, ready, due, service;
            infile >> cx;
            infile >> cy;
            infile >> demand;
            infile >> ready;
            infile >> due;
            infile >> service;

            customersX.push_back(cx);
            customersY.push_back(cy);
            demandsData.push_back(demand);
            earliestStartData.push_back(ready);
            latestEndData.push_back(due + service); // in input files due date is meant as latest start time
            serviceTimeData.push_back(service);
        }

        nbCustomers = customersX.size();

        computeDistanceMatrix(depotX, depotY, customersX, customersY);

        infile.close();
    }

    // Compute the distance matrix
    void computeDistanceMatrix(int depotX, int depotY, const vector<int>& customersX, const vector<int>& customersY) {
        distMatrixData.resize(nbCustomers);
        for (int i = 0; i < nbCustomers; ++i) {
            distMatrixData[i].resize(nbCustomers);
        }
        for (int i = 0; i < nbCustomers; ++i) {
            distMatrixData[i][i] = 0;
            for (int j = i + 1; j < nbCustomers; ++j) {
                double distance = computeDist(customersX[i], customersX[j], customersY[i], customersY[j]);
                distMatrixData[i][j] = distance;
                distMatrixData[j][i] = distance;
            }
        }

        distDepotData.resize(nbCustomers);
        for (int i = 0; i < nbCustomers; ++i) {
            distDepotData[i] = computeDist(depotX, customersX[i], depotY, customersY[i]);
        }
    }

    double computeDist(int xi, int xj, int yi, int yj) {
        return sqrt(pow((double)xi - xj, 2) + pow((double)yi - yj, 2));
    }
};

int main(int argc, char** argv) {
    if (argc < 2) {
        cerr << "Usage: cvrptw inputFile [outputFile] [timeLimit] [nbTrucks]" << endl;
        return 1;
    }

    const char* instanceFile = argv[1];
    const char* solFile = argc > 2 ? argv[2] : NULL;
    const char* strTimeLimit = argc > 3 ? argv[3] : "20";

    try {
        Cvrptw model;
        model.readInstance(instanceFile);
        model.solve(atoi(strTimeLimit));
        if (solFile != NULL)
            model.writeSolution(solFile);
        return 0;
    } catch (const exception& e) {
        cerr << "An error occurred: " << e.what() << endl;
        return 1;
    }
}

Compilation / Execution (Windows): copy %LS_HOME%binlocalsolvernet.dll .

csc Cvrptw.cs /reference:localsolvernet.dll

Cvrptw instancesR101.25.txt

using System;
using System.IO;
using System.Collections.Generic;
using localsolver;

public class Cvrptw : IDisposable
{
    // LocalSolver
    LocalSolver localsolver;

    // Number of customers
    int nbCustomers;

    // Capacity of the trucks
    int truckCapacity;

    // Latest allowed arrival to depot
    int maxHorizon;

    // Demand on each node
    List<int> demandsData;

    // Earliest arrival on each node
    List<int> earliestStartData;

    // Latest departure from each node
    List<int> latestEndData;

    // Service time on each node
    List<int> serviceTimeData;

    // Distance matrix between customers
    double[][] distMatrixData;

    // Distances between customers and depot
    double[] distDepotData;

    // Number of trucks
    int nbTrucks;

    // Decision variables
    LSExpression[] customersSequences;

    // Are the trucks actually used
    LSExpression[] trucksUsed;

    // Cumulated lateness in the solution (must be 0 for the solution to be valid)
    LSExpression totalLateness;

    // Number of trucks used in the solution
    LSExpression nbTrucksUsed;

    // Distance traveled by all the trucks
    LSExpression totalDistance;

    public Cvrptw()
    {
        localsolver = new LocalSolver();
    }

    /* Read instance data */
    void ReadInstance(string fileName)
    {
        ReadInputCvrptw(fileName);
    }

    public void Dispose()
    {
        if (localsolver != null)
            localsolver.Dispose();
    }

    void Solve(int limit)
    {
        // Declare the optimization model
        LSModel model = localsolver.GetModel();

        trucksUsed = new LSExpression[nbTrucks];
        customersSequences = new LSExpression[nbTrucks];
        LSExpression[] distRoutes = new LSExpression[nbTrucks];
        LSExpression[] endTime = new LSExpression[nbTrucks];
        LSExpression[] homeLateness = new LSExpression[nbTrucks];
        LSExpression[] lateness = new LSExpression[nbTrucks];

        // Sequence of customers visited by each truck
        for (int k = 0; k < nbTrucks; ++k)
            customersSequences[k] = model.List(nbCustomers);

        // All customers must be visited by the trucks
        model.Constraint(model.Partition(customersSequences));

        // Create LocalSolver arrays to be able to access them with an "at" operator
        LSExpression demands = model.Array(demandsData);
        LSExpression earliest = model.Array(earliestStartData);
        LSExpression latest = model.Array(latestEndData);
        LSExpression serviceTime = model.Array(serviceTimeData);
        LSExpression distDepot = model.Array(distDepotData);
        LSExpression distMatrix = model.Array(distMatrixData);

        for (int k = 0; k < nbTrucks; ++k)
        {
            LSExpression sequence = customersSequences[k];
            LSExpression c = model.Count(sequence);

            // A truck is used if it visits at least one customer
            trucksUsed[k] = c > 0;

            // The quantity needed in each route must not exceed the truck capacity
            LSExpression demandLambda = model.LambdaFunction(i => demands[sequence[i]]);
            LSExpression routeQuantity = model.Sum(model.Range(0, c), demandLambda);
            model.Constraint(routeQuantity <= truckCapacity);

            // Distance traveled by truck k
            LSExpression distLambda = model.LambdaFunction(
                i => distMatrix[sequence[i - 1], sequence[i]]
            );
            distRoutes[k] =
                model.Sum(model.Range(1, c), distLambda)
                + model.If(c > 0, distDepot[sequence[0]] + distDepot[sequence[c - 1]], 0);

            // End of each visit
            LSExpression endTimeLambda = model.LambdaFunction(
                (i, prev) =>
                    model.Max(
                        earliest[sequence[i]],
                        model.If(
                            i == 0,
                            distDepot[sequence[0]],
                            prev + distMatrix[sequence[i - 1], sequence[i]]
                        )
                    ) + serviceTime[sequence[i]]
            );

            endTime[k] = model.Array(model.Range(0, c), endTimeLambda);

            // Arriving home after max_horizon
            homeLateness[k] = model.If(
                trucksUsed[k],
                model.Max(0, endTime[k][c - 1] + distDepot[sequence[c - 1]] - maxHorizon),
                0
            );

            // Completing visit after latest_end
            LSExpression lateLambda = model.LambdaFunction(
                i => model.Max(endTime[k][i] - latest[sequence[i]], 0)
            );
            lateness[k] = homeLateness[k] + model.Sum(model.Range(0, c), lateLambda);
        }

        // Total lateness
        totalLateness = model.Sum(lateness);

        // Total nb trucks used
        nbTrucksUsed = model.Sum(trucksUsed);

        // Total distance traveled (convention in Solomon's instances is to round to 2 decimals)
        totalDistance = model.Round(100 * model.Sum(distRoutes)) / 100;

        // Objective: minimize the lateness, then the number of trucks used, then the distance traveled
        model.Minimize(totalLateness);
        model.Minimize(nbTrucksUsed);
        model.Minimize(totalDistance);

        model.Close();

        // Parametrize the solver
        localsolver.GetParam().SetTimeLimit(limit);

        localsolver.Solve();
    }

    /* Write the solution in a file with the following format:
     *  - number of trucks used and total distance
     *  - for each truck the customers visited (omitting the start/end at the depot) */
    void WriteSolution(string fileName)
    {
        using (StreamWriter output = new StreamWriter(fileName))
        {
            output.WriteLine(nbTrucksUsed.GetValue() + " " + totalDistance.GetDoubleValue());
            for (int k = 0; k < nbTrucks; ++k)
            {
                if (trucksUsed[k].GetValue() != 1)
                    continue;
                // Values in sequence are in [0..nbCustomers-1]. +1 is to put it back in [1..nbCustomers]
                // as in the data files (0 being the depot)
                LSCollection customersCollection = customersSequences[k].GetCollectionValue();
                for (int i = 0; i < customersCollection.Count(); ++i)
                    output.Write((customersCollection[i] + 1) + " ");
                output.WriteLine();
            }
        }
    }

    public static void Main(string[] args)
    {
        if (args.Length < 1)
        {
            Console.WriteLine("Usage: Cvrptw inputFile [solFile] [timeLimit]");
            Environment.Exit(1);
        }
        string instanceFile = args[0];
        string outputFile = args.Length > 1 ? args[1] : null;
        string strTimeLimit = args.Length > 2 ? args[2] : "20";

        using (Cvrptw model = new Cvrptw())
        {
            model.ReadInstance(instanceFile);
            model.Solve(int.Parse(strTimeLimit));
            if (outputFile != null)
                model.WriteSolution(outputFile);
        }
    }

    private string[] SplitInput(StreamReader input)
    {
        string line = input.ReadLine();
        if (line == null)
            return new string[0];
        return line.Split(new[] { ' ' }, StringSplitOptions.RemoveEmptyEntries);
    }

    // The input files follow the "Solomon" format
    private void ReadInputCvrptw(string fileName)
    {
        using (StreamReader input = new StreamReader(fileName))
        {
            string[] splitted;

            input.ReadLine();
            input.ReadLine();
            input.ReadLine();
            input.ReadLine();

            splitted = SplitInput(input);
            nbTrucks = int.Parse(splitted[0]);
            truckCapacity = int.Parse(splitted[1]);

            input.ReadLine();
            input.ReadLine();
            input.ReadLine();
            input.ReadLine();

            splitted = SplitInput(input);
            int depotX = int.Parse(splitted[1]);
            int depotY = int.Parse(splitted[2]);
            maxHorizon = int.Parse(splitted[5]);

            List<int> customersX = new List<int>();
            List<int> customersY = new List<int>();
            demandsData = new List<int>();
            earliestStartData = new List<int>();
            latestEndData = new List<int>();
            serviceTimeData = new List<int>();

            while (!input.EndOfStream)
            {
                splitted = SplitInput(input);
                if (splitted.Length < 7)
                    break;
                customersX.Add(int.Parse(splitted[1]));
                customersY.Add(int.Parse(splitted[2]));
                demandsData.Add(int.Parse(splitted[3]));
                int ready = int.Parse(splitted[4]);
                int due = int.Parse(splitted[5]);
                int service = int.Parse(splitted[6]);

                earliestStartData.Add(ready);
                latestEndData.Add(due + service); // in input files due date is meant as latest start time
                serviceTimeData.Add(service);
            }

            nbCustomers = customersX.Count;

            ComputeDistanceMatrix(depotX, depotY, customersX, customersY);
        }
    }

    // Compute the distance matrix
    private void ComputeDistanceMatrix(
        int depotX,
        int depotY,
        List<int> customersX,
        List<int> customersY
    )
    {
        distMatrixData = new double[nbCustomers][];
        for (int i = 0; i < nbCustomers; ++i)
            distMatrixData[i] = new double[nbCustomers];

        for (int i = 0; i < nbCustomers; ++i)
        {
            distMatrixData[i][i] = 0;
            for (int j = i + 1; j < nbCustomers; ++j)
            {
                double dist = ComputeDist(
                    customersX[i],
                    customersX[j],
                    customersY[i],
                    customersY[j]
                );
                distMatrixData[i][j] = dist;
                distMatrixData[j][i] = dist;
            }
        }

        distDepotData = new double[nbCustomers];
        for (int i = 0; i < nbCustomers; ++i)
            distDepotData[i] = ComputeDist(depotX, customersX[i], depotY, customersY[i]);
    }

    private double ComputeDist(int xi, int xj, int yi, int yj)
    {
        return Math.Sqrt(Math.Pow(xi - xj, 2) + Math.Pow(yi - yj, 2));
    }
}

Compilation / Execution (Windows): javac Cvrptw.java -cp %LS_HOME%binlocalsolver.jar

java -cp %LS_HOME%binlocalsolver.jar;. Cvrptw instancesR101.25.txt

Compilation / Execution (Linux): javac Cvrptw.java -cp /opt/localsolver_11_5/bin/localsolver.jar

java -cp /opt/localsolver_11_5/bin/localsolver.jar:. Cvrptw instances/R101.25.txt

import java.util.*;
import java.io.*;
import localsolver.*;

public class Cvrptw {
    // LocalSolver
    private final LocalSolver localsolver;

    // Number of customers
    int nbCustomers;

    // Capacity of the trucks
    private int truckCapacity;

    // Latest allowed arrival to depot
    int maxHorizon;

    // Demand on each node
    List<Integer> demandsData;

    // Earliest arrival on each node
    List<Integer> earliestStartData;

    // Latest departure from each node
    List<Integer> latestEndData;

    // Service time on each node
    List<Integer> serviceTimeData;

    // Distance matrix
    private double[][] distMatrixData;

    // Distances between customers and depot
    private double[] distDepotData;

    // Number of trucks
    private int nbTrucks;

    // Decision variables
    private LSExpression[] customersSequences;

    // Are the trucks actually used
    private LSExpression[] trucksUsed;

    // Distance traveled by each truck
    private LSExpression[] distRoutes;

    // End time array for each truck
    private LSExpression[] endTime;

    // Home lateness for each truck
    private LSExpression[] homeLateness;

    // Cumulated Lateness for each truck
    private LSExpression[] lateness;

    // Cumulated lateness in the solution (must be 0 for the solution to be valid)
    private LSExpression totalLateness;

    // Number of trucks used in the solution
    private LSExpression nbTrucksUsed;

    // Distance traveled by all the trucks
    private LSExpression totalDistance;

    private Cvrptw(LocalSolver localsolver) {
        this.localsolver = localsolver;
    }

    /* Read instance data */
    private void readInstance(String fileName) throws IOException {
        readInputCvrptw(fileName);
    }

    private void solve(int limit) {
        // Declare the optimization model
        LSModel m = localsolver.getModel();

        trucksUsed = new LSExpression[nbTrucks];
        customersSequences = new LSExpression[nbTrucks];
        distRoutes = new LSExpression[nbTrucks];
        endTime = new LSExpression[nbTrucks];
        homeLateness = new LSExpression[nbTrucks];
        lateness = new LSExpression[nbTrucks];

        // Sequence of customers visited by each truck.
        for (int k = 0; k < nbTrucks; ++k)
            customersSequences[k] = m.listVar(nbCustomers);

        // All customers must be visited by the trucks
        m.constraint(m.partition(customersSequences));

        // Create LocalSolver arrays to be able to access them with an "at" operator
        LSExpression demands = m.array(demandsData);
        LSExpression earliest = m.array(earliestStartData);
        LSExpression latest = m.array(latestEndData);
        LSExpression serviceTime = m.array(serviceTimeData);
        LSExpression distDepot = m.array(distDepotData);
        LSExpression distMatrix = m.array(distMatrixData);

        for (int k = 0; k < nbTrucks; ++k) {
            LSExpression sequence = customersSequences[k];
            LSExpression c = m.count(sequence);

            // A truck is used if it visits at least one customer
            trucksUsed[k] = m.gt(c, 0);

            // The quantity needed in each route must not exceed the truck capacity
            LSExpression demandLambda = m.lambdaFunction(i -> m.at(demands, m.at(sequence, i)));
            LSExpression routeQuantity = m.sum(m.range(0, c), demandLambda);
            m.constraint(m.leq(routeQuantity, truckCapacity));

            // Distance traveled by truck k
            LSExpression distLambda = m
                .lambdaFunction(i -> m.at(distMatrix, m.at(sequence, m.sub(i, 1)), m.at(sequence, i)));
            distRoutes[k] = m.sum(m.sum(m.range(1, c), distLambda), m.iif(m.gt(c, 0),
                m.sum(m.at(distDepot, m.at(sequence, 0)), m.at(distDepot, m.at(sequence, m.sub(c, 1)))), 0));

            // End of each visit
            LSExpression endTimeLambda = m.lambdaFunction((i, prev) -> m.sum(
                m.max(m.at(earliest, m.at(sequence, i)),
                    m.sum(m.iif(m.eq(i, 0), m.at(distDepot, m.at(sequence, 0)),
                        m.sum(prev, m.at(distMatrix, m.at(sequence, m.sub(i, 1)), m.at(sequence, i)))))),
                m.at(serviceTime, m.at(sequence, i))));

            endTime[k] = m.array(m.range(0, c), endTimeLambda);

            LSExpression theEnd = endTime[k];

            // Arriving home after max_horizon
            homeLateness[k] = m.iif(trucksUsed[k],
                m.max(0,
                    m.sum(m.at(theEnd, m.sub(c, 1)), m.sub(m.at(distDepot, m.at(sequence, m.sub(c, 1))), maxHorizon))),
                0);

            // completing visit after latest_end
            LSExpression lateLambda = m
                .lambdaFunction(i -> m.max(m.sub(m.at(theEnd, i), m.at(latest, m.at(sequence, i))), 0));
            lateness[k] = m.sum(homeLateness[k], m.sum(m.range(0, c), lateLambda));
        }

        totalLateness = m.sum(lateness);
        nbTrucksUsed = m.sum(trucksUsed);
        totalDistance = m.div(m.round(m.prod(100, m.sum(distRoutes))), 100);

        // Objective: minimize the number of trucks used, then minimize the distance traveled
        m.minimize(totalLateness);
        m.minimize(nbTrucksUsed);
        m.minimize(totalDistance);

        m.close();

        // Parametrize the solver
        localsolver.getParam().setTimeLimit(limit);

        localsolver.solve();
    }

    // Write the solution in a file with the following format:
    // - number of trucks used and total distance
    // - for each truck the customers visited (omitting the start/end at the depot)
    private void writeSolution(String fileName) throws IOException {
        try (PrintWriter output = new PrintWriter(fileName)) {
            output.println(nbTrucksUsed.getValue() + " " + totalDistance.getDoubleValue());
            for (int k = 0; k < nbTrucks; ++k) {
                if (trucksUsed[k].getValue() != 1)
                    continue;
                // Values in sequence are in [0..nbCustomers-1]. +1 is to put it back in [1..nbCustomers]
                // as in the data files (0 being the depot)
                LSCollection customersCollection = customersSequences[k].getCollectionValue();
                for (int i = 0; i < customersCollection.count(); ++i) {
                    output.print((customersCollection.get(i) + 1) + " ");
                }
                output.println();
            }
        }
    }

    // The input files follow the "Solomon" format
    private void readInputCvrptw(String fileName) throws IOException {
        try (Scanner input = new Scanner(new File(fileName))) {
            input.nextLine();
            input.nextLine();
            input.nextLine();
            input.nextLine();

            nbTrucks = input.nextInt();
            truckCapacity = input.nextInt();

            input.nextLine();
            input.nextLine();
            input.nextLine();
            input.nextLine();

            input.nextInt();
            int depotX = input.nextInt();
            int depotY = input.nextInt();
            input.nextInt();
            input.nextInt();
            maxHorizon = input.nextInt();
            input.nextInt();

            List<Integer> customersX = new ArrayList<Integer>();
            List<Integer> customersY = new ArrayList<Integer>();
            demandsData = new ArrayList<Integer>();
            earliestStartData = new ArrayList<Integer>();
            latestEndData = new ArrayList<Integer>();
            serviceTimeData = new ArrayList<Integer>();

            while (input.hasNextInt()) {
                input.nextInt();
                int cx = input.nextInt();
                int cy = input.nextInt();
                int demand = input.nextInt();
                int ready = input.nextInt();
                int due = input.nextInt();
                int service = input.nextInt();

                customersX.add(cx);
                customersY.add(cy);
                demandsData.add(demand);
                earliestStartData.add(ready);
                latestEndData.add(due + service);// in input files due date is meant as latest start time
                serviceTimeData.add(service);
            }

            nbCustomers = customersX.size();

            computeDistanceMatrix(depotX, depotY, customersX, customersY);

        }
    }

    // Computes the distance matrix
    private void computeDistanceMatrix(int depotX, int depotY, List<Integer> customersX, List<Integer> customersY) {
        distMatrixData = new double[nbCustomers][nbCustomers];
        for (int i = 0; i < nbCustomers; ++i) {
            distMatrixData[i][i] = 0;
            for (int j = i + 1; j < nbCustomers; ++j) {
                double dist = computeDist(customersX.get(i), customersX.get(j), customersY.get(i), customersY.get(j));
                distMatrixData[i][j] = dist;
                distMatrixData[j][i] = dist;
            }
        }

        distDepotData = new double[nbCustomers];
        for (int i = 0; i < nbCustomers; ++i) {
            distDepotData[i] = computeDist(depotX, customersX.get(i), depotY, customersY.get(i));
        }
    }

    private double computeDist(int xi, int xj, int yi, int yj) {
        return Math.sqrt(Math.pow(xi - xj, 2) + Math.pow(yi - yj, 2));
    }

    public static void main(String[] args) {
        if (args.length < 1) {
            System.err.println("Usage: java Cvrptw inputFile [outputFile] [timeLimit] [nbTrucks]");
            System.exit(1);
        }

        try (LocalSolver localsolver = new LocalSolver()) {
            String instanceFile = args[0];
            String outputFile = args.length > 1 ? args[1] : null;
            String strTimeLimit = args.length > 2 ? args[2] : "20";

            Cvrptw model = new Cvrptw(localsolver);
            model.readInstance(instanceFile);
            model.solve(Integer.parseInt(strTimeLimit));
            if (outputFile != null) {
                model.writeSolution(outputFile);
            }
        } catch (Exception ex) {
            System.err.println(ex);
            ex.printStackTrace();
            System.exit(1);
        }
    }
}

Источник

From Wikipedia, the free encyclopedia

A figure illustrating the vehicle routing problem

The vehicle routing problem (VRP) is a combinatorial optimization and integer programming problem which asks «What is the optimal set of routes for a fleet of vehicles to traverse in order to deliver to a given set of customers?» It generalises the travelling salesman problem (TSP). It first appeared in a paper by George Dantzig and John Ramser in 1959,^[1] in which the first algorithmic approach was written and was applied to petrol deliveries. Often, the context is that of delivering goods located at a central depot to customers who have placed orders for such goods. The objective of the VRP is to minimize the total route cost. In 1964, Clarke and Wright improved on Dantzig and Ramser’s approach using an effective greedy algorithm called the savings algorithm.

Determining the optimal solution to VRP is NP-hard,^[2] so the size of problems that can be optimally solved using mathematical programming or combinatorial optimization may be limited. Therefore, commercial solvers tend to use heuristics due to the size and frequency of real world VRPs they need to solve.

VRP has many direct applications in industry. Vendors of VRP routing tools often claim that they can offer cost savings of 5%–30%.^[3]

Setting up the problem[edit]

The VRP concerns the service of a delivery company. How things are delivered from one or more depots which has a given set of home vehicles and operated by a set of drivers who can move on a given road network to a set of customers. It asks for a determination of a set of routes, S, (one route for each vehicle that must start and finish at its own depot) such that all customers’ requirements and operational constraints are satisfied and the global transportation cost is minimized. This cost may be monetary, distance or otherwise.^[2]

The road network can be described using a graph where the arcs are roads and vertices are junctions between them. The arcs may be directed or undirected due to the possible presence of one way streets or different costs in each direction. Each arc has an associated cost which is generally its length or travel time which may be dependent on vehicle type.^[2]

To know the global cost of each route, the travel cost and the travel time between each customer and the depot must be known. To do this our original graph is transformed into one where the vertices are the customers and depot, and the arcs are the roads between them. The cost on each arc is the lowest cost between the two points on the original road network. This is easy to do as shortest path problems are relatively easy to solve. This transforms the sparse original graph into a complete graph. For each pair of vertices i and j, there exists an arc (i,j) of the complete graph whose cost is written as $C_{ij}$ and is defined to be the cost of shortest path from i to j. The travel time $t_{{ij}}$ is the sum of the travel times of the arcs on the shortest path from i to j on the original road graph.

Sometimes it is impossible to satisfy all of a customer’s demands and in such cases solvers may reduce some customers’ demands or leave some customers unserved. To deal with these situations a priority variable for each customer can be introduced or associated penalties for the partial or lack of service for each customer given ^[2]

The objective function of a VRP can be very different depending on the particular application of the result but a few of the more common objectives are:^[2]

Minimize the global transportation cost based on the global distance travelled as well as the fixed costs associated with the used vehicles and drivers
Minimize the number of vehicles needed to serve all customers
Least variation in travel time and vehicle load
Minimize penalties for low quality service
Maximize a collected profit/score.

VRP variants[edit]

A map showing the relationship between common VRP subproblems.

Several variations and specializations of the vehicle routing problem exist:

Vehicle Routing Problem with Profits (VRPP): A maximization problem where it is not mandatory to visit all customers. The aim is to visit once customers maximizing the sum of collected profits while respecting a vehicle time limit. Vehicles are required to start and end at the depot. Among the most known and studied VRPP, we cite:
- The Team Orienteering Problem (TOP) which is the most studied variant of the VRPP,^[4]^[5]^[6]
- The Capacitated Team Orienteering Problem (CTOP),
- The TOP with Time Windows (TOPTW).
Vehicle Routing Problem with Pickup and Delivery (VRPPD): A number of goods need to be moved from certain pickup locations to other delivery locations. The goal is to find optimal routes for a fleet of vehicles to visit the pickup and drop-off locations.
Vehicle Routing Problem with LIFO: Similar to the VRPPD, except an additional restriction is placed on the loading of the vehicles: at any delivery location, the item being delivered must be the item most recently picked up. This scheme reduces the loading and unloading times at delivery locations because there is no need to temporarily unload items other than the ones that should be dropped off.
Vehicle Routing Problem with Time Windows (VRPTW): The delivery locations have time windows within which the deliveries (or visits) must be made.
Capacitated Vehicle Routing Problem: CVRP or CVRPTW. The vehicles have a limited carrying capacity of the goods that must be delivered.
Vehicle Routing Problem with Multiple Trips (VRPMT): The vehicles can do more than one route.
Open Vehicle Routing Problem (OVRP): Vehicles are not required to return to the depot.
Inventory Routing Problem (IRP): Vehicles are responsible for satisfying the demands in each delivery point ^[7]
Multi-Depot Vehicle Routing Problem (MDVRP): Multiple depots exist from which vehicles can start and end.^[8]

Several software vendors have built software products to solve various VRP problems. Numerous articles are available for more detail on their research and results.

Although VRP is related to the Job Shop Scheduling Problem, the two problems are typically solved using different techniques.^[9]

Exact solution methods[edit]

There are three main different approaches to modelling the VRP

Vehicle flow formulations—this uses integer variables associated with each arc that count the number of times that the edge is traversed by a vehicle. It is generally used for basic VRPs. This is good for cases where the solution cost can be expressed as the sum of any costs associated with the arcs. However it can’t be used to handle many practical applications.^[2]
Commodity flow formulations—additional integer variables are associated with the arcs or edges which represent the flow of commodities along the paths travelled by the vehicles. This has only recently been used to find an exact solution.^[2]
Set partitioning problem—These have an exponential number of binary variables which are each associated with a different feasible circuit. The VRP is then instead formulated as a set partitioning problem which asks what is the collection of circuits with minimum cost that satisfy the VRP constraints. This allows for very general route costs.^[2]

Vehicle flow formulations[edit]

The formulation of the TSP by Dantzig, Fulkerson and Johnson was extended to create the two index vehicle flow formulations for the VRP

${text{min}}sum _{iin V}sum _{jin V}c_{ij}x_{ij}$

subject to

${displaystyle sum _{iin V}x_{ij}=1quad forall jin Vbackslash left{0right}}$

(1)

${displaystyle sum _{jin V}x_{ij}=1quad forall iin Vbackslash left{0right}}$

(2)

${displaystyle sum _{iin {Vbackslash left{0right}}}x_{i0}=K}$

(3)

${displaystyle sum _{jin {Vbackslash left{0right}}}x_{0j}=K}$

(4)

${displaystyle sum _{inotin S}sum _{jin S}x_{ij}geq r(S),~~forall Ssubseteq Vsetminus {0},Sneq emptyset }$

(5)

${displaystyle x_{ij}in {0,1}quad forall i,jin V}$

(6)

In this formulation $c_{ij}$ represents the cost of going from node to node , $x_{ij}$ is a binary variable that has value if the arc going from to is considered as part of the solution and otherwise, is the number of available vehicles and corresponds to the minimum number of vehicles needed to serve set . We are also assuming that is the depot node.

Constraints 1 and 2 state that exactly one arc enters and exactly one leaves each vertex associated with a customer, respectively. Constraints 3 and 4 say that the number of vehicles leaving the depot is the same as the number entering. Constraints 5 are the capacity cut constraints, which impose that the routes must be connected and that the demand on each route must not exceed the vehicle capacity. Finally, constraints 6 are the integrality constraints.^[2]

One arbitrary constraint among the constraints is actually implied by the remaining ones so it can be removed. Each cut defined by a customer set is crossed by a number of arcs not smaller than (minimum number of vehicles needed to serve set ).^[2]

An alternative formulation may be obtained by transforming the capacity cut constraints into generalised subtour elimination constraints (GSECs).

${displaystyle sum _{iin S}sum _{jin S}x_{ij}leq |S|-r(S)}$

which imposes that at least arcs leave each customer set .^[2]

GCECs and CCCs have an exponential number of constraints so it is practically impossible to solve the linear relaxation. A possible way to solve this is to consider a limited subset of these constraints and add the rest if needed.

A different method again is to use a family of constraints which have a polynomial cardinality which are known as the MTZ constraints, they were first proposed for the TSP ^[10] and subsequently extended by Christofides, Mingozzi and Toth.^[11]

${displaystyle u_{j}-u_{i}geq d_{j}-C(1-x_{ij})~~~~~~forall i,jin Vbackslash {0},ineq j~~~~{text{s.t. }}d_{i}+d_{j}leq C}$

${displaystyle 0leq u_{i}leq C-d_{i}~~~~~~forall iin Vbackslash {0}}$

where $u_i,~i in V backslash {0}$ is an additional continuous variable which represents the load left in the vehicle after visiting customer and $d_{i}$ is the demand of customer . These impose both the connectivity and the capacity requirements. When $x_{{ij}}=0$ constraint then is not binding’ since and whereas $x_{ij} = 1$ they impose that .

These have been used extensively to model the basic VRP (CVRP) and the VRPB. However, their power is limited to these simple problems. They can only be used when the cost of the solution can be expressed as the sum of the costs of the arc costs. We cannot also know which vehicle traverses each arc. Hence we cannot use this for more complex models where the cost and or feasibility is dependent on the order of the customers or the vehicles used.^[2]

Manual versus automatic optimum routing[edit]

There are many methods to solve vehicle routing problems manually. For example, optimum routing is a big efficiency issue for forklifts in large warehouses. Some of the manual methods to decide upon the most efficient route are: Largest gap, S-shape, Aisle-by-aisle, Combined and Combined +. While Combined + method is the most complex, thus the hardest to be used by lift truck operators, it is the most efficient routing method. Still the percentage difference between the manual optimum routing method and the real optimum route was on average 13%.^[12]^[13]

Metaheuristic[edit]

Due to the difficulty of solving to optimality large-scale instances of vehicle routing problems, a significant research effort has been dedicated to metaheuristics such as Genetic algorithms, Tabu search, Simulated annealing and Adaptive Large Neighborhood Search (ALNS). Some of the most recent and efficient metaheuristics for vehicle routing problems reach solutions within 0.5% or 1% of the optimum for problem instances counting hundreds or thousands of delivery points.^[14] These methods are also more robust in the sense that they can be more easily adapted to deal with a variety of side constraints. As such, the application of metaheuristic techniques is often preferred for large-scale applications with complicating constraints and decision sets.

Classification of Solution Strategies[edit]

Most solutions to the vehicle routing problems can be classified as one of the following approaches:^[15]

References[edit]

^ Dantzig, George Bernard; Ramser, John Hubert (October 1959). «The Truck Dispatching Problem» (PDF). Management Science. 6 (1): 80–91. doi:10.1287/mnsc.6.1.80.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l Toth, P.; Vigo, D., eds. (2002). The Vehicle Routing Problem. Monographs on Discrete Mathematics and Applications. Vol. 9. Philadelphia: Society for Industrial and Applied Mathematics. ISBN 0-89871-579-2.
^ Geir Hasle; Knut-Andreas Lie; Ewald Quak, eds. (2007). Geometric Modelling, Numerical Simulation, and Optimization:: Applied Mathematics at SINTEF. Berlin: Springer Verlag. pp. 397–398. ISBN 978-3-540-68783-2.
^ Chao, I-Ming; Golden, Bruce L; Wasil, Edward A (1996). «The Team Orienteering Problem». European Journal of Operational Research. 88 (3): 464–474. doi:10.1016/0377-2217(94)00289-4.
^ Archetti, C.; Sperenza, G.; Vigo, D. (2014). «Vehicle routing problems with profits». In Toth, P.; Vigo, D. (eds.). Vehicle Routing: Problems, Methods, and Applications (Second ed.). pp. 273–297. doi:10.1137/1.9781611973594.ch10.
^ Hammami, Farouk; Rekik, Monia; Coelho, Leandro C. (2020). «A hybrid adaptive large neighborhood search heuristic for the team orienteering problem». Computers & Operations Research. 123: 105034. doi:10.1016/j.cor.2020.105034. S2CID 221134904.
^ Ekici, Ali; Özener, Okan Örsan; Kuyzu, Gültekin (November 2015). «Cyclic Delivery Schedules for an Inventory Routing Problem». Transportation Science. 49 (4): 817–829. doi:10.1287/trsc.2014.0538.
^ Mahmud, Nafix; Haque, Md. Mokammel (February 2019). Solving Multiple Depot Vehicle Routing Problem (MDVRP) using Genetic Algorithm. 2019 International Conference on Electrical, Computer and Communication Engineering (ECCE). doi:10.1109/ECACE.2019.8679429.
^ Beck, J.C.; Prosser, P.; Selensky, E. (2003). «Vehicle routing and job shop scheduling: What’s the difference?» (PDF). Proceedings of the 13th International Conference on Artificial Intelligence Planning and Scheduling.
^ Miller, C. E.; Tucker, E. W.; Zemlin, R. A. (1960). «Integer Programming Formulations and Travelling Salesman Problems». J. ACM. 7: 326–329. doi:10.1145/321043.321046. S2CID 2984845.
^ Christofides, N.; Mingozzi, A.; Toth, P. (1979). The Vehicle Routing Problem. Chichester, UK: Wiley. pp. 315–338.
^ «Why Is Manual Warehouse Optimum Routing So Inefficient?». Locatible.com. 2016-09-26. Retrieved 2016-09-26.
^ Roodbergen, Kees Jan (2001). «Routing methods for warehouses with multiple cross aisles» (PDF). roodbergen.com. Retrieved 2016-09-26.
^ Vidal T, Crainic TG, Gendreau M, Prins C (2014). «A unified solution framework for multi-attribute vehicle routing problems». European Journal of Operational Research. 234 (3): 658–673. doi:10.1016/j.ejor.2013.09.045. S2CID 21037953.
^ Bodin, Lawrence; Golden, Bruce (1981). «Classification in vehicle routing and scheduling». Networks. 11 (2): 97–108. doi:10.1002/net.3230110204.

What Are the Common VRPs?

Below are some of the real-life VRPs field service businesses often face in day-to-day operations.

Vehicle Routing Problem with Time Windows (VRPTWs)

Customers often demand that their deliveries be made during a specific period. This limits pick-up and delivery times, as your driver has to show up at a customer’s door within a prioritized timeframe.

Note, the driver can arrive before the scheduled delivery time, but never outside the set time window.

Falling behind schedule will annoy your customers and will cause increased customer attrition and a significant drop in the revenue and profit margin.

So, you need to factor in time windows in the most cost-efficient way, while planning your routes. That’s what VRPTW is all about.

Time windows can be:

Soft time windows: Serving outside the time window is allowed, but it comes with hefty penalties.

Hard time windows: Time violations are not allowed at all. A driver must wait if he or she arrives way ahead of the scheduled time until the time window opens and cannot show up late.

Disjoint time windows: Showing up between two time windows, a driver has to wait until the next time window opens.

Multiple time windows: A set of non-overlapping time windows with different lengths.

Now, let’s understand this with a real-life scenario and the approach to a solution.

Real-Life Scenario

Let’s take the example of FedEx. A parcel has arrived at the destination country and is accepted by a last-mile carrier.

The package needs to be moved to the distribution center. From there, a courier will take the parcel to deliver it to a customer who will be waiting for it on Wednesday, from 10 to 11 in the morning. This doesn’t look like a soft time window, right?

So, the courier driver cannot afford to be late. But, 15 other packages need to be delivered, each with a specified timeframe as well.

VRPTWs must be solved everywhere, from postal, restaurant, or supermarket deliveries to security patrol services and bus routing.

Approach to Solution

Now, how can the driver show up on time everywhere, while taking the shortest routes?

We need to connect the dots: Identify a set of routes with the least traveling expenses and maximal customer satisfaction which, in this case, can be achieved by adhering to the prioritized time windows.

Pickup and Delivery Vehicle Routing Problem (PDVRP)

On-demand delivery businesses, such as courier delivery and food delivery companies, need to plan delivery routes each day; sometimes even multiple times a day, depending on the nature and scale of the business.

Several resource constraints, parameters, and schedules need to be considered while chalking out these routes.

Usually, with PDVRP, the challenge is combining delivery and pickup points to help reduce travel time and cut fuel costs.

An ideal route should pair delivery and pickup points while keeping the route the shortest or fastest one possible.

Real-Life Scenario

Let’s consider the example of Uber. The system needs to assign drivers to locations efficiently so that it doesn’t take much time to reach there and pick up a customer.

Approach to Solution

Assign routes to the drivers or vehicles to pick up and deliver passengers. The customer’s request must be met as soon as possible by reducing the total length of the vehicle’s routes.

Capacity Constraint Vehicle Routing Problem (CVRP)

Each vehicle has a maximum load capacity (both weight and volume) which must be considered. So, it is often challenging to save costs by loading more items and serving more customers in one trip without exceeding the vehicle’s capacity.

There might also be additional complications, such as:

The varying sizes of parcels for delivery and pickup,
The different capacities of all the vehicles, and multiple depots
Multiple depots
Multi-compartment vehicles

Real-Life Scenario

Take Tesco, a grocery and general merchandise retailer, as an example. They use over-the-road vehicles for good distribution. They transport the goods on pallets and each vehicle can accommodate only a limited number of pallets, while each business unit (BU) demands a different number of pallets. For example, a large retail store requires several times more pallets than the vehicle can fit.

Approach to Solution

The best approach should be assigning the shortest routes so that the total amount of units for the vehicle meets its capacity limitations.

[By Lady-Shirakawa. CC BY-SA 3.0, Link]

Why Is the VRP Difficult to Solve?

Although we have described the above VRPs in isolation, they are often combined in real life, thus exploding the overall size of the problem.

For instance, the placement of delivery and pickup addresses in a route affects whether you will have enough space in your vehicle for another pickup.

Also, if you do have space, adding or leaving out another pickup or delivery will impact your time window for other customers.

So, solving the VRP is difficult even for the most experienced dispatchers and seasoned drivers. Because it is a combinatorial optimization problem where the contributing factors are sometimes uncertain, unaccounted for, and cannot be predicted.

Why Do You Need An Effective Solution for VRP?

The primary reason why you need an effective VRP solution is to reduce logistics expenses. There are other reasons include the following:

It helps achieve sustainable growth.
It boosts efficiency and productivity.
It saves time as well as increases customer satisfaction, thereby increasing revenue and improving profitability.

How to Solve the Vehicle Routing Problem?

There are a couple of solutions to address the VRP, such as:

Manual Solving (including Google Maps)

Based on previous experience, the ideal driver should be able to pull off a route plan manually. But, that will be a time-consuming and nerve-racking task to do.

Additionally, there’s a high probability that the drivers will make mistakes during the manual process. Simply put, manual solving is the most inefficient method to address the VRP.

A free route planner like Google Maps cannot help either. It would be able to guide your driver to the best route considering traffic but cannot provide the right order that your driver should follow to deliver all the packages on time.

The Google Maps route planner is not intended for everyday use, especially when you are managing a large fleet of vehicles with 100 or more deliveries. Such a basic tool can only address some of the routing problems.

Learn if Google Maps is right for your delivery business.

Preset Solvers

This is a faster and better method than solving the VRP manually. However, preset solvers only satisfy or solve two or three basic constraints. It can only be applied in “academic settings” that require in-depth research, but not in the real world.

Route Optimization Software

A route optimization software is the best solution to solve the VRP.

With a route planner, the unsolvable VRPs and all the constraints can be addressed in less than 30 seconds. It will even give you optimal routes that are faster, save fuel, cut costs, and adhere to the time windows of each customer.

A delivery route planner is a cost-effective and scalable solution that offers multi-vehicle and multi-stop routing as well as ensures the safety of deliveries and your drivers.

Want To See For Yourself How Route4Me Can Boost Your Profits?

Whether you want to slash the time it takes you to plan routes for your drivers, increase the number of stops they can make, or keep your customers satisfied knowing that your drivers show up on time… Route4Me helps you achieve that!

Start Free 7 Day Trial

How to Choose the Right Map Route Planner to Solve the VRP?

While assessing the different route planners, pay attention to the ones that offer the following core functionalities:

Visualization of Route Plans

Route planning is a visual process. This means that being able to see where each customer location is, which driver will serve it, and how inserting or deleting an address will impact the overall route will make route planning much more seamless.

So, find VRP software that can help you modify routes on the fly.

Advanced Algorithm

A route planner app should come with an AI-powered algorithm that will create optimal routes with accurate directions to work by considering all the constraints, including traffic jams, specific time windows, vehicle load capacities, and pickup and delivery schedules, while, at the same time, saving on fuel and drive time.

Proof Of Delivery

The best route planners come with an eSignature feature that helps drivers capture electronic customer signatures and store or save them as digital proof of delivery. So, you must consider this feature.

ALSO READ: Proof of Delivery – Advantages and Benefits

Real-Time Tracking

When it comes to your field service business, knowing the location of your vehicles and drivers is crucial.

For instance, if a field rep is behind the schedule, you can track the vehicles in real-time to find out the reason and understand how the delay will affect the ETAs of the remaining deliveries.

You can then either re-adjust the routes instantly or inform the customers about the updated ETAs. This will enhance your customer service and increase the accountability of your drivers.

So, GPS tracking is a must for every field service business.

ALSO READ: 4 Ways Vehicle Location Tracking Can Reduce Your Expenses and Improve Productivity

Geocoding Capabilities

You wouldn’t want your drivers to end up at the wrong address or waste time searching for the right address. That’s why you need a route planner app that comes with geocoding capabilities.

A geocoder auto-corrects any wrong addresses entered into the system so you never need to worry about the accuracy of the customers’ addresses.

ALSO READ: How To Eliminate Costly Mistakes Caused By Incorrect Addresses And Drop-off Locations

In order to ensure that you pick a delivery scheduling software that really works for you, consider eighteen more points as laid out in our article: How to Choose the Best Route Planner.

Conclusion about the Vehicle Routing Problem

No matter how experienced your managers and drivers are, you can’t always anticipate what will happen on the road and adjust your route instantly to meet your customers’ unanticipated requests.

So, you need an advanced tech solution to plan your routes as well as track your drivers and vehicles. Essentially, using an advanced route optimizer is the most efficient way to resolve your VRPs and make planning and modifying routes seem like a walk in the park!

Do you have any questions about the vehicle routing problem? Please feel free to leave your comments below.

Want To See For Yourself How Route4Me Can Boost Your Profits?

Start Free 7 Day Trial

Источник

VRPTW Example

Create the data

Python

C++

Java

C#

Time callback

Python

C++

Java

C#

Add time window constraints

Python

C++

Java

C#

Set search parameters

Python

C++

Java

C#

Add the solution printer

Python

C++

Java

C#

Solution windows

Solve

Python

C++

Java

C#

Running the program

Save the solution windows to a list or array

Python

C++

Python

C++

Complete programs

Python

C++

Java

C#

Principles learned¶

Problem¶

Data¶

Program¶

Setting up the problem[edit]

VRP variants[edit]

Exact solution methods[edit]

Vehicle flow formulations[edit]

Manual versus automatic optimum routing[edit]

Metaheuristic[edit]

Classification of Solution Strategies[edit]

See also[edit]

References[edit]

Further reading[edit]

Table of Contents

What Are the Common VRPs?

Vehicle Routing Problem with Time Windows (VRPTWs)

Real-Life Scenario

Approach to Solution

Pickup and Delivery Vehicle Routing Problem (PDVRP)

Real-Life Scenario

Approach to Solution

Capacity Constraint Vehicle Routing Problem (CVRP)

Real-Life Scenario

Approach to Solution

Why Is the VRP Difficult to Solve?

Why Do You Need An Effective Solution for VRP?

How to Solve the Vehicle Routing Problem?

Manual Solving (including Google Maps)

Preset Solvers

Route Optimization Software

Want To See For Yourself How Route4Me Can Boost Your Profits?

How to Choose the Right Map Route Planner to Solve the VRP?

Visualization of Route Plans

Advanced Algorithm

Proof Of Delivery

Real-Time Tracking