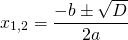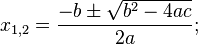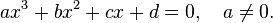Windows forms c решение квадратного уравнения - Доктор Windows

Сегодня мы напишем программу, которая выведет нам решение квадратного уравнения на С#. Сделаем мы всё это в Windows Forms. В программе мы найдём дискриминант и оба корня.

Для создания программы нам понадобится знание начальной школы и трёх формул.

Формула нахождения дискриминанта:

Формула нахождения корней выражения, если дискриминант больше нуля:

И формула нахождения одного корня выражения, если дискриминант равен нулю:

Ну и, пожалуй, стоит вспомнить сам вид квадратного выражения:

Теперь пора приступать к программе.

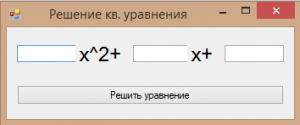
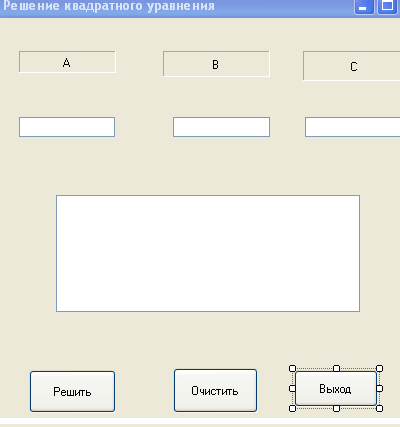
Для начала создаём незамысловатую форму под наши нужды:

Здесь у нас 3 TextBox’a, 2 Label’a и 1 кнопка Button. Выводить решение мы будем в отдельном MessageBox’е.

Приступаем к коду. Дважды щёлкаем на Button и в открывшемся участке кода начинаем писать.

Сначала объявляем переменные, которым будут присвоены значения,введённые пользователем в TextBox’ы:

double a = Convert.ToDouble(textBox1.Text);

double b = Convert.ToDouble(textBox2.Text);

double c = Convert.ToDouble(textBox3.Text);

Конвертируем данные из TextBox’ов в тип повышенной точности с плавающей точкой double, так как они имеют строковый тип, а нам нужен числовой.

Затем объявляем дискриминант и пишем его формулу:

double d = b * b — 4 * a * c;

Мы знает три варианта развития событий при решении дискриминанта:

1) Если дискриминант больше нуля, то уравнение имеет два корня.

2) Если дискриминант равен нулю, то уравнение имеет лишь один корень.

3) Если дискриминант меньше нуля, то уравнение не имеет корней вообще.

Теперь перенесём написанное нами в код благодаря оператору условия if:

if (d < 0)

{

MessageBox.Show(«Дискриминант меньше нуля. Корней нет.»); }

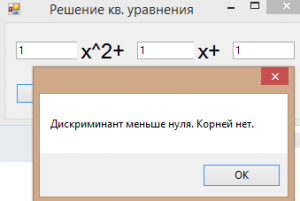
Если мы введём в нашу форму числа, нажмём кнопку «Решить уравнение» и окажется, что дискриминант будет меньше нуля, то программа нам выдаст в новом окне вот такое сообщение:

Теперь создадим условие, если дискриминант равен нулю:

if(d == 0)

{

double x=(—b/(2*a));

MessageBox.Show(«Дискриминант равен нулю. Корень равен «+x+«.»);

}

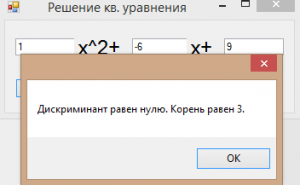
Мы создаём переменную, в которую занесётся решение формулы , а потом выводим эту переменную в MessageBox. Обратите внимание на форму записи такого вывода. Простой текст выводится в кавычках, а переменные выводятся при обрамлении их плюсами.

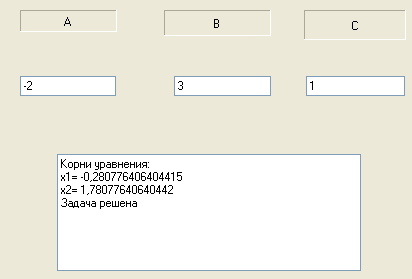
Вывод будет вот такой:

Ну и, наконец, условие, когда дискриминант больше нуля:

if(d > 0)

{

double x1 = ((—b — Math.Sqrt(d)) / (2 * a));

double x2 = ((—b + Math.Sqrt(d)) / (2 * a));

MessageBox.Show(«Дискриминант равен « +d+ «. Первый корень равен «+x1+«. Второй корень равен «+x2+«.»);

}

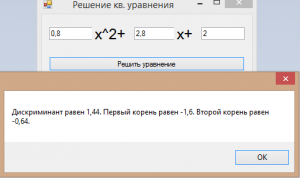
Считаем корни по формуле и выводим их точно так же, как было описано выше.

Вот так работает наша программа, выдающая решение квадратного уравнения на С#. Исходный код программы ниже:

Скачать исходник

Источник

50 / 35 / 16

Регистрация: 24.10.2016

Сообщений: 956

Решение квадратного уравнения

20.01.2021, 14:16. Показов 2327. Ответов 7

Здравствуйте!!! Помогите пожалуйста довести до конца прогу, задание звучит так: Реализовать программу, которая находит корни квадратного уравнения ax2+bx+c=0 или сообщает об отсутствии корней. Задать специальный переключатель для решения уравнения в действительных или комплексных числах
первую часть я сделал, но вторую часть не могу допилить, в с# новичок
https://yadi.sk/d/QnARFHW1eV273

__________________
Помощь в написании контрольных, курсовых и дипломных работ, диссертаций здесь

50 / 35 / 16

Регистрация: 24.10.2016

Сообщений: 956

21.01.2021, 12:04

[ТС]

помогите кто-нибудь))

8923 / 4835 / 1885

Регистрация: 11.02.2013

Сообщений: 10,246

21.01.2021, 16:01

Держи.

50 / 35 / 16

Регистрация: 24.10.2016

Сообщений: 956

21.01.2021, 19:32

[ТС]

ViterAlex, а что за ответы странные)))

Миниатюры

8923 / 4835 / 1885

Регистрация: 11.02.2013

Сообщений: 10,246

21.01.2021, 19:55

Не знаю, у меня всё правильно

Миниатюры

50 / 35 / 16

Регистрация: 24.10.2016

Сообщений: 956

21.01.2021, 20:07

[ТС]

ViterAlex, у меня ругается на символы $, у меня visual studio 2010

ViterAlex

8923 / 4835 / 1885

Регистрация: 11.02.2013

Сообщений: 10,246

21.01.2021, 20:11

Сообщение было отмечено никмейн как решение

Решение

А, у тебя студия старая, там старая версия C#, поэтому интерполяция строки не работает. Значит надо переписывать через string.Format:

private void button1_Click(object sender, EventArgs e)
{
    double a = Convert.ToDouble(textBox1.Text);
    double b = Convert.ToDouble(textBox2.Text);
    double c = Convert.ToDouble(textBox3.Text);
    var eq = new QuadraticEq(a, b, c);
    if (chbSolveComplex.Checked)
    {
        var result = eq.SolveComplex();
        var stringResult = string.Empty;
        if (result[0] == result[1])
        {
            stringResult = string.Format("x1=x2={0:f2}", result[0]);
        }
        else
        {
            stringResult = string.Format("x1 = {0:f2}rnx2 = {1:f2}", result[0], result[1]);
        }
        lblResult.Text = stringResult;
    }
    else
    {
        var result = eq.Solve();
        var stringResult = string.Empty;
        if (double.IsNaN(result[0]))
        {
            stringResult = "Нет вещественных корней";
        }
        else if (Math.Abs(result[0] - result[1]) <= double.Epsilon)
        {
            stringResult = string.Format("x1=x2={0:f2}", result[0]);
        }
        else
        {
            stringResult = string.Format("x1 = {0:f2}rnx2 = {1:f2}", result[0], result[1]);
        }
        lblResult.Text = stringResult;
    }
}

50 / 35 / 16

Регистрация: 24.10.2016

Сообщений: 956

21.01.2021, 20:12

[ТС]

на картинке

Миниатюры

IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604	21.01.2021, 20:12
8

Источник

Установленные визуальные компоненты
и свойства

labelA

labelB

labelC

textBoxA

textBoxB

textBoxC

textBoxRez

buttonReh

buttonCl

Установка
свойств labelA,
labelB, labelC

(name)

ForeColor

Text

TextAlign

AutoSize

Установка
свойств
textBoxA, textBoxB, textBoxC

(name)

Установка
свойств textBoxRez

(name)

Multiline

Установка
свойств
buttonReh, buttonCl

(name)

Text

Компонент
TextBox

AceptsReturn –
нажатие
Enter создает
новую
строку

Lines
– строки

Multiline
–несколько строк

ReadOnly
– только для чтения

ScrollBars
– полоса прокрутки

TextAlign
— выравнивание

WordWrap
– перенос символов без нажатия Enter

Методы TextBox

AppendText
– добавление текста

Clear
–очистка

Copy
– копирование выбранных строк

Select
– выбор заданного текста

Show
– компонент делается видимым

using
System;

using
System.Collections.Generic;

using
System.ComponentModel;

using
System.Data;

using
System.Drawing;

using
System.Text;

using
System.Windows.Forms;

namespace
KvadratUravnenie

{

public
partial
class
Form1
: Form

{

public
Form1()

{

InitializeComponent();

}

private
void
button1_Click(object
sender, EventArgs
e)

{

double
a, b, c, d, x1, x2;

//textBox4.Text
= «»;

a
= Convert.ToDouble(textBox1.Text);

b
= Convert.ToDouble(textBox2.Text);

c
= Convert.ToDouble(textBox3.Text);

d
= b * b — 4 * a * c;

if
(d >= 0)

{

d
= Math.Sqrt(d);

x1
= (-b + d) / (2 * a);

x2
= (-b — d) / (2 * a);

textBox4.Text
+= «Корни
уравнения:
rn»;

textBox4.Text
+= «x1=
»
+ x1.ToString()+»rn»;

textBox4.Text
+= «nx2=
»
+ x2.ToString()+»rn»;

textBox4.AppendText(«Задача
решена»);

}

else

textBox4.Text
= «Нет
действительных
корней»;

}

private
void
button2_Click(object
sender, EventArgs
e)

{

textBox1.Text
= «»;

textBox2.Text
= «»;

textBox3.Text
= «»;

textBox4.Text
= «»;

}

private
void
button3_Click(object
sender, EventArgs
e)

{

Close();

}

Соседние файлы в предмете Информатика

Источник

Решение квадратного уравнения

Решение квадратного уравнения
Помогите, пожалуйста, как написать код для решения этого уравнения на С# в window form? Даны.

При клике по кнопке, решение квадратного уравнения не выводится в label
Пожалуйста помогите. Мне нужно помочь с кусочком проекта) В одной из форм моего проекта нужно.

Полное исследование квадратного уравнения ax2 + bx + c = 0 и биквадратного уравнения ax4 + bx2 + c = 0
Создание простейших приложений for Windows. Полное исследование квадратного уравнения ax2 +.

Нахождение корней квадратного уравнения
Напишите программу нахождения корней квадратного уравнения a × x2 + b × x + c = 0.

Вложения

kv_yravnenie.zip (11.7 Кб, 17 просмотров)

Решение

Нахождение корней квадратного уравнения
Подскажите, а как можно данную задачу сделать в WindowsForn? Приложение для нахождения корней.

Отобразить на экране монитора график квадратного уравнения
Отобразить на экране монитора график квадратного уравнения, имеющего действительные корни. График.

Проблема с минусом при коэффициентах квадратного уравнения
Здравствуйте, уважаемые программисты. Писал я, значит, программу, решающую квадратные уравнения, и.

Регулярные выражения для парсинга чисел из квадратного уравнения
составляю регулярные выражения для «выдергивания» чисел из квадратного уравнения. регулярное.

Источник

Приложение для решения квадратных уравнений

Метод Ньютона для решения нелинейных уравнений
В общем, помогите составить программу в Win.Form для решения нелинейных уравнений методом Ньютона.

Метод Ньютона для решения нелинейных уравнений
Помогите написать код для решения уравнений данным методом

Проектирование и выбор решения для реализации (локальное; клиентское приложение)
Вступление для Админов. Куда засунуть эту тему я не нашёл (разделов по проектированию нет (или я.

если в этом же классе.
просто вариант. (попробуй, не проверял)
скинь архив с формой.

Добавлено через 27 минут

Вложения

TheSQR_Equatation.zip (41.0 Кб, 143 просмотров)

Нахождение максимального значения корня среди действительных корней квадратных уравнений
(Написать программу, осуществляющую заданные вычисления с использованием процедур. Вид используемых.

Консольное приложение для решения квадратных уравнений, исправить код
Всем здрасте. Только начал изучать C# и решил написать простенькое консольное приложение для.

Программа для решения квадратных уравнений
Здравствуйте! Я написал программу, решающую квадратные уравнения. Все работает. Только есть одна.

Источник

Программирование на C, C# и Java

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Для создания программы нам понадобится знание начальной школы и трёх формул.

Формула нахождения дискриминанта:

Формула нахождения корней выражения, если дискриминант больше нуля:

И формула нахождения одного корня выражения, если дискриминант равен нулю:

Ну и, пожалуй, стоит вспомнить сам вид квадратного выражения:

Теперь пора приступать к программе.

Для начала создаём незамысловатую форму под наши нужды:

Здесь у нас 3 TextBox’a, 2 Label’a и 1 кнопка Button. Выводить решение мы будем в отдельном MessageBox’е.

Приступаем к коду. Дважды щёлкаем на Button и в открывшемся участке кода начинаем писать.

Сначала объявляем переменные, которым будут присвоены значения,введённые пользователем в TextBox’ы:

Источник

Программа для решения квадратных уравнений на C++

Довольно часто в пособиях по программированию встречаются задания по нахождению решений каких-нибудь математических уравнений. Задача нахождения корней квадратного уравнения — это довольно тривиальная задача, как и многие другие задачи. Решается она очень просто при помощи листа бумаги и ручки, но решение можно автоматизировать посредством написания прикладной программы и её использования. В этой статье мы напишем такую программу.

Алгоритм решения квадратного уравнения

Существуют различные способы решения квадратных уравнений, но мы рассмотрим решение через дискриминант.

Существует несколько условий:

Просим пользователя ввести значения переменных и сохраняем каждое значение

Проверяем условие, если дискриминант больше или равен 0, то находим корни и выводим

в противном случае выводим сообщение

На этом всё, осталось скомпилировать, запустить и проверить. Запускаем и вводим данные, чтобы D был меньше 0

Ответы тоже верны. Программа работает правильно.

Ниже представлен весь листинг программы для нахождения корней квадратного уравнения на C++

Для вас это может быть интересно:

Программа для решения квадратных уравнений на C++ : 24 комментария

Программировать так сложно…

Не так сложно, как Вам кажется! Немного литературы, немного практики и смотреть на код решения такой задачи Вы будете по-другому.

Ответил вам по электронной почте

Критику принимаете? 🙂
Программа дырявая как сито.

Если число очень маленькое, но положительное, например 10^(-20) — у вас будет переполнение или типо того. Оператор > проверяет знак числа (это отдельный бит), а оператор == для дробных чисел не имеет смысла, т.к. в младших разрядах числа обычно находится какой-нибудь мусор, который при таком сравнении дает false.

Тут есть три вопроса:
1) зачем два раза вычислять одно и тоже (я про корень)
2) что делать если мне корни надо как-то использовать, а не просто вывести (тут есть проблема, ведь у меня то один корень — то два). Чтобы лучше понять в чем проблема — попробуйте вынести вычисление корней в отдельную функцию. У вас то вообще, если корень один — то их выведется все равно два, одинаковых.
3) в переменной «a» может быть ноль (или близкое к нулю число) — при этом мы получим деление на ноль (а точнее, переполнение).

Вообще, эта задача — прекрасный пример для юнит-тестирования и демонстрации принципов разработки через тестирование. Именно его я рассматривал в своей статье по теме тестирования: Юнит-тестирование. Пример. Boost Unit Test. Дело в том, что тут куча вариантов сделать ошибку, при этом их понимание приходит не сразу, т.е. школьник решая задачу напишет по формуле которой учили (ну и вот как у вас). А потом надо разбираться и смотреть как программа может сломаться, при этом разрабатывать тесты.

Принимаем 🙂
Согласен с вами во всём! Программу можно реализовать намного лучше, используя различные проверки и валидацию входных данных.
Однако, статья рассчитана на аудиторию, которая только начинает познавать программирование или делает лабораторную. 🙂 Чтобы людям легче было понять, реализация данной программы упрощена до невозможности. И, возможно, несправедливо было с моей стороны не предупредить их о возможных ошибках в работе программы, которые могут вскрыться позже, если подать на вход определенные значения.
Кстати, у вас интересная статья по тестированию!

Пожалуйста подскажите как ввести экран правильный ответ дискриминанта

Помогите решить в Dev C++
Sqrt x^2+1+sqrt|x|,x0

Здравствуйте, можете помочь с решением биквадратного и триквадратного уравнения?

#include
using namespace std;
int main()
<
/*Решение квадратных уравнений*/
setlocale(0, «»);
cout a;
cout <> b;
cout <> c;
D = pow(b, 2) — 4 * a * c;
cout

Уважаемая, Лена! Я, надеюсь, вы знаете, что код программы, написанной на языке программирования C++ нельзя тупо вставить в блокнот и сохранить под названием «cpp.sh»? Если не знали, то я, видимо, открыл для вас Америку!

iconcerts где забыл
#include

if (d >= 0) <
xfst = ((-b + sqrt(d)) / double(2 * a));
xscd = ((-b — sqrt(d)) / double(2 * a));
std::cout

Создать программу для решения квадратного уравнения.
У меня не получаеться, но и копифейсом я не хочу заниматься.
Прошу помогите. Заранее спасибо.

Давайте напишем действительно полезную программу! Вы наверняка уже устали считать дискриминант для квадратных уравнений? Давайте автоматизируем этот процесс.

На вход программы подаются три целых числа — коэффициенты уравнения ax^2 + bx + c = 0ax
2
+bx+c=0

Гарантируется, что a neq 0a

=0.

Выведите через пробел корни уравнения в порядке убывания и округленные «вниз». Если уравнение имеет корень кратности 2 — выведите одно число. Если у уравнения нет действительных корней — выведите «NO»

Для извлечения корней используйте функцию sqrt. Она содержится в библиотеке сmath ( она уже импортирована в коде ). Для округления воспользуйтесь функцией floor ( из той же библиотеки ).

1 2 2
Sample Output 2:

Пожалуйста подскажите как ввести экран ответ дискриминанта

Пожалуйста подскажите как ввести на екран ответь дискриминанта

Подскажите как правильно решить?
Обчислити z = (x1 + y1) / (x2 + y2), де х1, х2 — коренi рiвняння 2х^2 + x — 4 =0.
y1, y2 — коренi рiвняння ay^2 + 2y — 1 = 0. Усi коренi дiйснi.

using namespace std;

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Источник

Нахождение корней квадратного уравнения

Как построить график квадратного уравнения?
как построить график квадратного уравнения?

Отобразить на экране монитора график квадратного уравнения
Отобразить на экране монитора график квадратного уравнения, имеющего действительные корни. График.

Enifan, это со школы ведь еще

Добавлено через 35 секунд

При клике по кнопке, решение квадратного уравнения не выводится в label
Пожалуйста помогите. Мне нужно помочь с кусочком проекта) В одной из форм моего проекта нужно.

Источник

Программирование на C, C# и Java

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

Решение квадратного уравнения на С# в Windows Forms.

Для создания программы нам понадобится знание начальной школы и трёх формул.

Формула нахождения дискриминанта:

Формула нахождения корней выражения, если дискриминант больше нуля:

И формула нахождения одного корня выражения, если дискриминант равен нулю:

Ну и, пожалуй, стоит вспомнить сам вид квадратного выражения:

Теперь пора приступать к программе.

Для начала создаём незамысловатую форму под наши нужды:

Здесь у нас 3 TextBox’a, 2 Label’a и 1 кнопка Button. Выводить решение мы будем в отдельном MessageBox’е.

Приступаем к коду. Дважды щёлкаем на Button и в открывшемся участке кода начинаем писать.

Сначала объявляем переменные, которым будут присвоены значения,введённые пользователем в TextBox’ы:

Решение квадратного уравнения

Уравнение вида a⋅x 2 + b⋅x + c = 0 — квадратное уравнение.

a, b, c — действительные числа, a ≠ 0.

Для того чтобы вычислить корни квадратного уравнения, нужно сначала найти дискриминант.

D = b 2 — 4⋅a⋅c;

если D 0, то уравнение имеет два действительных корня:
- x₁ = (-b + √D) / (2⋅a);
- x₂ = (-b + √D) / (2⋅a).

Поиск по сайту

Выражение вида f(x)=0 называется уравнением. Число х называется корнем уравнения, если при его подстановке уравнение обращается в верное равенство. В статье рассмотрим методы решения уравнений — как точных, так и численных (приближенных).

Решение квадратных уравнений

Квадратным уравнением называется уравнение вида

Классическая формула для нахождения его корней (действительных и комплексных):

где выражение D = b 2 − 4ac называется дискриминантом уравнения, от его значения зависит количество и характер решений:

Если D>0, то корней уравнения будет два и оба они будут действительными числами;
Если D=0, то будет лишь один дейсвительный корень уравнения;
Если D 2 +10x+200=0; данное уравнение не имеет действительных корней, но имеет пару сопряженных комплексных корней: x₁ = -1-6,2449979983984i, x₂ = -1+6,2449979983984i;
x 2 -8x+16=0; данное уравнение имеет один двукратный корень x₁=x₂=4;
x 2 -5x+6=0; данное уравнение имеет два различных корня x₁=2, x₂=3.

Напишем программу для решения этих уравнений:

На выходе получим:

5x^2 — 10x + 200 = 0
x0 = (-1, -6,2449979983984)
x1 = (-1, 6,2449979983984)

x^2 — 8x + 16 = 0
x0 = (4, 0)
x1 = (4, 0)

x^2 — 5x + 6 = 0
x0 = (3, 0)
x1 = (2, 0)

Воспользуемся WolframAlpha для проверки значений:

Решение кубических уравнений

Кубическим уравнением называется уравнение третьего порядка, которое имеет вид

Кубическое уравнение всегда имеет 3 корня, которые могут быть как вещественными, так и комплексными. Для решения кубических уравнений используется метод Виета-Кардано.

Формулы Кардано и Виета требуют применения специальных функций, и в том случае, когда требуется провести большую серию вычислений корней кубического уравнения с не слишком сильно меняющимися коэффициентами, более быстрым алгоритмом является использование метода Ньютона или других итерационных методов (с нахождением начального приближения по формулам Кардано-Виета), о которых мы поговорим дальше.

Рассмотрим в качестве примера следующие кубические уравнения:

x^3 — 6x^2 + 11x — 6 = 0
x^3 — 6x^2 + 11x + 6 = 0

Напишем программу для решения кубических уравнений с помощью метода Виета-Кардано:

Напишем программу для тестирования метода:

x^3 — 6x^2 + 11x — 6 = 0
x0 = (1, 0)
x1 = (3, 0)
x2 = (2, 0)

x^3 — 6x^2 + 11x + 6 = 0
x0 = (-0,434841368216901, 0)
x1 = (3,21742068410845, 1,85643189109788)
x2 = (3,21742068410845, -1,85643189109788)

Решим эти же уравнения с помощью WolframAlpha.

Решение биквадратных уравнений

Биквадратное уравнение — уравнение четвёртой степени вида

где a,b,c — заданные комплексные числа и a != 0. Подстановкой y = x 2 сводится к квадратному уравнению относительно y. Такой переход от одной неизвестной величины к другой называется методом замены неизвестных.

Рассмотрим в качестве примера кубические уравнения:

5x^4 — 10x^2 + 200 = 0
x^4 — 8x^2 + 16 = 0
x^4 — 5x^2 + 6 = 0

Таким образом немного модифицируем первую функцию для решения биквадратных уравнений:

Напшем программу для тестирования метода:

На выходе получим такие результаты:

5x^4 — 10x^2 + 200 = 0
x0 = (1,63164875514566, -1,91370783040891)
x1 = (-1,63164875514566, 1,91370783040891)
x2 = (1,63164875514566, 1,91370783040891)
x3 = (-1,63164875514566, -1,91370783040891)

x^4 — 8x^2 + 16 = 0
x0 = (2, 0)
x1 = (-2, 0)
x2 = (2, 0)
x3 = (-2, 0)

x^4 — 5x^2 + 6 = 0
x0 = (1,73205080756888, 0)
x1 = (-1,73205080756888, 0)
x2 = (1,4142135623731, 0)
x3 = (-1,4142135623731, 0)

По ссылкам раз, два, три можно убедиться в правильности решений.

источники:

http://programm.top/c-sharp/programs/quadratic-equation/

http://msugvnua000.web710.discountasp.net/Posts/Details/4394

Источник

Приветствую всех сегодня рассмотрим пример решения квадратного уравнения. Их часто задают в университетах, а так же в школах старших классов. Для начала посмотрим на условия задания: Написать программу вычисления корней квадратного уравнения вида ax2+bx+c = 0. Значения a, b и c вводить в режиме диалога. Предусмотреть проверку существования корней уравнения и выдать соответствующие сообщения. Для решения задачи использовать метод-процедуру. Зная задание приступим его решению.

Рассмотрим код программы:

//изучаем C# на nookery.ru

static void Main(string[] args)

{

// Ввод данных уравнения — значения a, b и c

// После ввода данных мы обрезаем лишние пробелы по краям методом Trim()

// и преобразовываем тип string во float

Console.Write(«Введите значение a = «);

float a = float.Parse(Console.ReadLine().Trim());

Console.Write(«Введите значение b = «);

float b = float.Parse(Console.ReadLine().Trim());

Console.Write(«Введите значение c = «);

float c = float.Parse(Console.ReadLine().Trim());

// Вычисление дискриминанта

float d = b * b — 4 * a * c;

// При дискриминанте меньшим 0 — выводим ошибку

if (d < 0)

{

Console.Write(«Дискриминант d < 0<!— hu —>. Решение квадратного уравнения невозможно.»);

}

else

{

// Объявляем корни уравнения

float x1, x2;

// При дискриминанте равным 0 оба корня равны

if (d == 0)

{

x1 = x2 = —(b / 2 * a);

}

else

{

// Извлекаем корень из дискриминанта

float sqrtD = (float)System.Math.Sqrt(d);

// Высчитываем корни уравнения

x1 = (—b + sqrtD) / (2 * a);

x2 = (—b — sqrtD) / (2 * a);

}

// Выводим результат

Console.Write(«d = « + d.ToString() + » x1 = « + x1.ToString() + » x2 = « + x2.ToString());

}

// Ждем нажатия клавиши, чтобы завершить выполнение программы

Console.ReadLine();

}

Код приведенный выше для решения квадратного уравнения, за комментирован с достаточно полным разъяснением, при написании программы не должно возникнуть никаких проблем.

Источник

Программирование на C, C# и Java

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

Решение квадратного уравнения на С# в Windows Forms.

Для создания программы нам понадобится знание начальной школы и трёх формул.

Формула нахождения дискриминанта:

Формула нахождения корней выражения, если дискриминант больше нуля:

И формула нахождения одного корня выражения, если дискриминант равен нулю:

Ну и, пожалуй, стоит вспомнить сам вид квадратного выражения:

Теперь пора приступать к программе.

Для начала создаём незамысловатую форму под наши нужды:

Здесь у нас 3 TextBox’a, 2 Label’a и 1 кнопка Button. Выводить решение мы будем в отдельном MessageBox’е.

Приступаем к коду. Дважды щёлкаем на Button и в открывшемся участке кода начинаем писать.

Сначала объявляем переменные, которым будут присвоены значения,введённые пользователем в TextBox’ы:

Решение квадратного уравнения

Уравнение вида a⋅x 2 + b⋅x + c = 0 — квадратное уравнение.

a, b, c — действительные числа, a ≠ 0.

Для того чтобы вычислить корни квадратного уравнения, нужно сначала найти дискриминант.

D = b 2 — 4⋅a⋅c;

если D 0, то уравнение имеет два действительных корня:
- x₁ = (-b + √D) / (2⋅a);
- x₂ = (-b + √D) / (2⋅a).

Программа для решения квадратных уравнений на C++

Алгоритм решения квадратного уравнения

Многие знают, что уравнение вида ax 2 + bx + c = 0 , где a не равно 0, называют квадратным уравнением.

Существуют различные способы решения квадратных уравнений, но мы рассмотрим решение через дискриминант.

Обозначается дискриминант буквой D . Из школьного курса знаем, что D = b 2 — 4ac .

Существует несколько условий:

Если D > 0, то решение имеет 2 различных вещественных корня.
Если D = 0, то оба вещественных корня равны.
Если D для вводавывода в консоли, #include для работы с математическими функциями и область using namespace std;

Просим пользователя ввести значения переменных и сохраняем каждое значение

Проверяем условие, если дискриминант больше или равен 0, то находим корни и выводим

в противном случае выводим сообщение

На этом всё, осталось скомпилировать, запустить и проверить. Запускаем и вводим данные, чтобы D был меньше 0

В этом случае D = 3*3 — 4*2*3 = -15, а это меньше 0, значит ответ программа дала верный.

Ответы тоже верны. Программа работает правильно.

Ниже представлен весь листинг программы для нахождения корней квадратного уравнения на C++

Для вас это может быть интересно:

Программа для решения квадратных уравнений на C++ : 24 комментария

Программировать так сложно…

Nicknixer Автор записи 15.10.2016

Доброго времени суток! Помогите пожалуйста написать программу, которая считает сколько символов в ряде двумерного массива. То есть , например массив 5 на 5, сколько символов в 1 ряде, сколько во 2 и т.д.

Ответил вам по электронной почте

Критику принимаете? 🙂
Программа дырявая как сито.

x = ( -1*b + sqrt(b*b — 4*a*c) ) / (2 * a);
x = ( -1*b — sqrt(b*b — 4*a*c) ) / (2 * a);

Но это ведь еще не все. Что будет если и «a» и «b» равны нулю? — тебе надо рассмотреть два варианта — если c = 0 (условно, близко к нулю), то корней бесконечно много. А если c != 0, то корней нет.

Николай Сергейчук Автор записи 09.02.2017

Николай, доброго времени суток! Можете помочь с написанием програмки в с++? 1-1/2!+1/3!-1/4!+1/5! и так до 1/100! ? Чтобы при заднии в строке номера члена последовательности выдавал сумму до него по такой вот формуле? Буду очень благодарен!

Пожалуйста подскажите как ввести экран правильный ответ дискриминанта

Помогите решить в Dev C++
Sqrt x^2+1+sqrt|x|,x0

Здравствуйте, можете помочь с решением биквадратного и триквадратного уравнения?

#include
using namespace std;
int main()
<
/*Решение квадратных уравнений*/
setlocale(0, «»);
cout a;
cout <> b;
cout <> c;
D = pow(b, 2) — 4 * a * c;
cout

ну и? если даже тупо скопировать код и вставить его в cpp.sh , ничего не работает. поебота какая то этот с++

помогите решить. заданы 3 перемены a.b.c записать вы радение на С
< 7a/b+2a, если a=b,
Х= < -34, если a>b,
< 3a/(2b-100), если a>b и а не равно != с

iconcerts где забыл
#include

Я ради интереса написал программу нахождения корней квадратного уравнения на С++, с выводом корней как в десятичном виде, так и в виде простой дроби (причём уже сокращённой), потому что выводя корни в десятичном виде программа их одновременно сокращает и округляет и 1/3 превращается в 0.333333 хотя на самом деле 0.333333 (3), то есть для проверки правильно ли нашёл корни ваш ребёнок, вы с получите что-то типа: X1= 0.285714; X2=0.214286, а на самом деле это будет X1=2/7; X2=3/14, кроме того, если корень из дискриминанта не получается целым числом, вы уже получите двойную неточность: сначала при извлечении корня программа отсечёт значение до 4-6 цифр после запятой с округлением, а затем сделает то же самое при делении числителя на знаменатель. Я и здесь сделал вывод корней в двух значениях: в десятичном и в виде выражения X1= (-b + sqrt(D))/(2*a); X2= (-b — sqrt(D))/(2*a), то есть выводится примерно вот так X1=-5+sqrt(21)/2; X2=-5-sqrt(21)/2 с одновременным разложением дискриминанта под корнем на множители, вынесением этих множителей из-под корня, если они выносятся нацело, их перемножением и дальнейшим сокращением. Вот, например, имеем a=3, b=15, c=3, при решении получаем D=189 программа выдаёт десятичные корни X1= -0.208712 и X2= -4.79129, а в виде выражения имеем: X1= -5+sqrt(21)/2, то есть первоначально получаем: X1= -15+sqrt(189)/6, -> 189=21*9 -> -15+3sqrt(21)/6 далее идёт сокращение на 3 и итог -5+sqrt(21)/2

День добрый.
Недавно начал изучать C++. Решил попробовать написать решение квадратного уравнения именно через оператор вида «условие ? выполняется : не выполняется». Т.е. если условие выполняется, то имеем два решения (даже если d = 0, то тоже должно быть два решения x1 = x2), если d a;
std::cout <> b;
std::cout <> c;
d = pow(b, 2) — 4 * a*c;
d >= 0 ? xfst = ((-b + sqrt(d)) / double(2 * a)) , xscd = ((-b — sqrt(d)) / double(2 * a)) : std::cout

Николай Сергейчук Автор записи 12.02.2020

if (d >= 0) <
xfst = ((-b + sqrt(d)) / double(2 * a));
xscd = ((-b — sqrt(d)) / double(2 * a));
std::cout

Здравствуйте! Как решить эту задачу? Приведенный пример сверху не подходит .

На вход программы подаются три целых числа — коэффициенты уравнения ax^2 + bx + c = 0ax
2
+bx+c=0

Гарантируется, что a neq 0a

=0.

1 0 -4
Sample Output 1:

2 -2
Sample Input 2:

1 2 2
Sample Output 2:

Пожалуйста подскажите как ввести экран ответ дискриминанта

Пожалуйста подскажите как ввести на екран ответь дискриминанта

using namespace std;

int main() <
double a = 2, b, c = -4;
int x1, x2;
double a1, b1 = 2, c1 = -1;
int y1, y2;
float z;

if((b*b — 4*a*c) >= 0 ) <
x1 = ( -1*b + sqrt(b*b — 4*a*c)) / (2 * a);
cout a1;

if((b1*b1 — 4*a1*c1) >= 0) <
y1 = ( -1*b1 + sqrt(b1*b1 — 4*a1*c1)) / (2 * a1);
cout = 0, y1 >= 0, y2 >= 0) <
z = (x1 + y1)/(x2 +y2);
cout

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

источники:

http://programm.top/c-sharp/programs/quadratic-equation/

http://nicknixer.ru/programmirovanie/programma-dlya-resheniya-kvadratnyx-uravnenij-na-c/

Источник